如果奇函数f(x) 是[3,7]上是增函数且最小值为5,那么f(x)在区间[-7,-3]上是( )
| A.增函数且最小值为-5 | B.减函数且最小值是-5 |
| C.增函数且最大值为-5 | D.减函数且最大值是-5 |
设 是实数,若复数
是实数,若复数 (
( 为虚数单位)在复平面内对应的点在直线
为虚数单位)在复平面内对应的点在直线 上,则
上,则 的值为()
的值为()
A.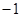 |
B. |
C.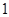 |
D. |
如图,已知正方体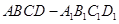 的棱长是1,点
的棱长是1,点 是对角线
是对角线 上一动点,记
上一动点,记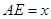 (
( ),过点
),过点 平行于平面
平行于平面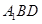 的截面将正方体分成两部分,其中点
的截面将正方体分成两部分,其中点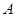 所在的部分的体积为
所在的部分的体积为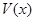 ,则函数
,则函数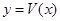 的图像大致为( )
的图像大致为( )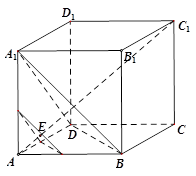
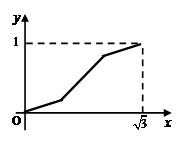
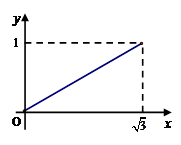
A B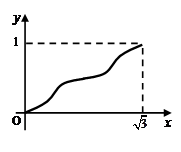

C D
给出下列命题,其中真命题的个数是( )
①存在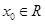 ,使得
,使得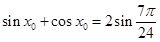 成立;
成立;
②对于任意的三个平面向量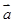 、
、 、
、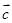 ,总有
,总有 成立;
成立;
③相关系数 (
(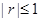 ),
), 值越大,变量之间的线性相关程度越高.
值越大,变量之间的线性相关程度越高.
| A.0 | B.1 | C.2 | D.3 |
如图,函数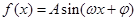 (其中
(其中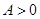 ,
,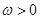 ,
,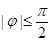 )与坐标轴的三个交点
)与坐标轴的三个交点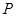 、
、 、
、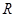 满足
满足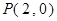 ,
,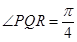 ,
,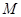 为
为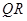 的中点,
的中点,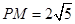 ,则
,则 的值为( )
的值为( )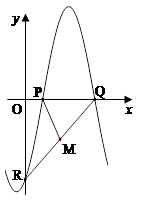
A. |
B. |
C.8 | D.16 |
设 ,则
,则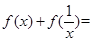 ( )
( )
A. |
B.2 | C.3 | D.4 |