同时抛掷15枚均匀的硬币一次
(1)试求至多有1枚正面向上的概率;
(2)试问出现正面向上为奇数枚的概率与出现正面向上为偶数枚的概率是否相等?
请说明理由.
设全集为R,集合 ,
,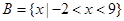 .
.
(1)求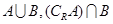 ;
;
(2)已知 ,若
,若 ,求实数
,求实数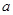 的取值范围.
的取值范围.
设数列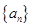 的前
的前 项和为
项和为 ,已知
,已知 ,
, ,
,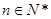 .
.
(1)求数列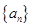 的通项公式;
的通项公式;
(2)证明:对一切正整数 ,有
,有 .
.
(本小题满分13分)已知椭圆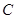 :
: (
( )的焦距为
)的焦距为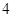 ,且过点
,且过点 .
.
(1)求椭圆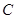 的方程和离心率;
的方程和离心率;
(2)设 (
( )为椭圆
)为椭圆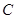 上一点,过点
上一点,过点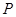 作
作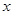 轴的垂线,垂足为
轴的垂线,垂足为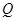 .取点
.取点 ,连 结
,连 结 ,过点
,过点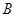 作
作 的垂线交
的垂线交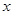 轴于点
轴于点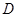 ,点
,点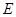 是点
是点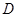 关于
关于 轴的对称点.试判断直线
轴的对称点.试判断直线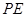 与椭圆
与椭圆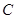 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
(本小题满分13分)已知函数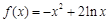 .
.
(1)求函数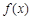 的最大值;
的最大值;
(2)若函数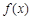 与
与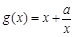 有相同极值点,
有相同极值点,
(ⅰ)求实数 的值;
的值;
(ⅱ)若对于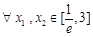 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本题满分12分)如图,四边形PDCE为矩形,ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD= CD=1,PD=
CD=1,PD=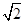 .
.
(1)若M为PA中点,求证:AC∥平面MDE;
(2)求直线PA与平面PBC所成角的正弦值;
(3)在线段PC上是否存在一点Q(除去端点),使得平面QAD与平面PBC所成锐二面角的大小为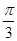 ?
?