棱柱ABC―A1B1C1中,AC⊥BC,∠AB1C=α,∠ABC=β,∠BAB1=θ,则
| A.sinα=sinβcosθ | B.cosα=cosβcosθ |
| C.cosβ=cosαcosθ | D.sinβ=sinαcosβ |
半径为6的圆与x轴相切,且与圆x2+(y-3)2=1内切,则此圆的方程是( )
| A.(x-4)2+(y-6)2=6 | B.(x 4)2+(y-6)2=6 4)2+(y-6)2=6 |
| C.(x-4)2+(y-6)2=36 | D.(x 4)2+(y-6)2=36 4)2+(y-6)2=36 |
两圆x2+y2=r2,(x-3)2+(y+1)2=r2外切、则正实数r的值是( )
A. |
B. |
C. |
D.5 |
两圆x2+y2-6x=0和x2+y2+8y+12=0的位置关系是( )
| A.相离 | B.外切 |
| C.相交 | D.内切 |
 表示的曲线为( )
表示的曲线为( )
| A.两个半圆 | B.一个圆 |
| C.半个圆 | D.两个圆 |
若直线3x+4y-12=0与x轴交 于A点, 与y轴于交B点,那么 OAB的内切圆方程是( )
OAB的内切圆方程是( )
A.x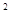 +y +y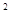 +2x+2y+1=0 +2x+2y+1=0 |
B.x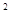 +y +y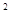 -2x+2y+1=0 -2x+2y+1=0 |
C.x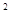 +y +y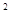 -2x-2y+1=0 -2x-2y+1=0 |
D.x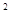 +y +y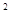 -2x-2y-1=0 -2x-2y-1=0 |