如下图,在空间直角坐标系中BC=2,原点O是BC的中点,点A的坐标是(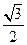 ,
,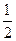 ,0),点D在平面yoz上,且
,0),点D在平面yoz上,且 BDC=900,
BDC=900, DCB=300,求点D的坐标。
DCB=300,求点D的坐标。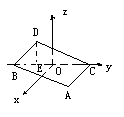
在△ABC中,角A,B,C 的对边分别是 ,已知
,已知
(1)求角B的大小
(2)求三角形ABC的面积。
在△ABC中, a、b、c分别是角A、B、C的对边,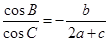 ,
,
(Ⅰ)求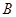 的值;
的值;
(Ⅱ)若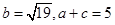 ,求
,求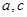 的值
的值
已知不等式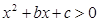 的解集为
的解集为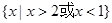
(1)求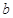 和
和 的值; (2)求不等式
的值; (2)求不等式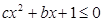 的解集
的解集
已知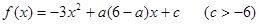
(1)若关于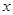 的不等式
的不等式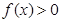 的解集是(-1,3),求实数
的解集是(-1,3),求实数 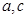 的值。
的值。
(2)解关于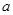 的不等式
的不等式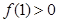
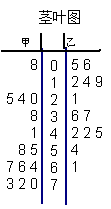
为了调查甲、乙两个网站受欢迎的程度,随机选取了14天,统计上午8:00—10:00间各自的点击量,得如下所示的统计图,根据统计图:
(1)甲、乙两个网站点击量的极差分别是多少?
(2)甲网站点击量在[10,40]间的频率是多少?
(3)甲、乙两个网站哪个更受欢迎?并说明理由。