对“四地六校”的高二年段学生是爱好体育还是爱好文娱进行调查，共调查了40人，其中男生25人，女生15人。男生中有15人爱好体育，另外10人爱好文娱。女生中有5人爱好体育，另外10人爱好文娱；
（1）根据以上数据制作一个2×2的列联表；
（2）在多大的程度上可以认为性别与是否爱好体育有关系？
附：
（此公式也可写成
）
参考数据：
 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
 |
1.323 |
2.072 |
2. 706 |
3. 841 |
5. 024 |
某种产品的广告费用支出
与销售额
之间有如下的对应数据：
|
2 |
4 |
5 |
6 |
8 |
|
30 |
40 |
50 |
60 |
70 |
（1）求对的回归直线方程；
（2）据此估计广告费用为10销售收入的值。
已知函数
（1）求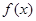
的单调递减区间；
（2）若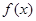在区间
上的最大值为20，求它在该区间上的最小值
设z＝lg(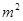
－2m－2)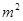＋(＋3m＋2)i，m∈R，当m为何值时，z分别满足：
(1)是实数； (2)是纯虚数； (3)z>0.
求证：
的解集为
和
的值； (2)求不等式
的解集