在直三棱柱ABC—A1B1C1中,CA=CB=CC1=2,∠ACB=90°,E、F分别是BA、BC的中点,G是AA1上一点,且AC1⊥EG.
(Ⅰ)确定点G的位置;
(Ⅱ)求直线AC1与平面EFG所成角θ的大小. 
已知以点C(1,﹣2)为圆心的圆与直线x+y﹣1=0相切.
(1)求圆C的标准方程;
(2)求过圆内一点P(2,﹣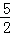 )的最短弦所在直线的方程.
)的最短弦所在直线的方程.
在△ABC中,角A,B,C所对的边分别为a,b,c,已知b=3,c=8,角A为锐角,△ABC的面积为6 .
.
(1)求角A的大小;
(2)求a的值.
已知三角形的三个顶点是A(4,0),B(6,6),C(0,2).
(1)求AB边上的高所在直线的方程;
(2)求AC边上的中线所在直线的方程.
设各项为正数的数列 的前
的前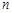 和为
和为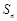 ,且
,且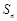 满足:
满足: .等比数列
.等比数列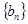 满足:
满足: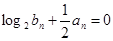 .
.
(Ⅰ)求数列 ,
,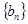 的通项公式;
的通项公式;
(Ⅱ)设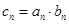 ,求数列
,求数列 的前
的前 项的和
项的和 ;
;
(Ⅲ)证明:对一切正整数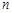 ,有
,有 .
.
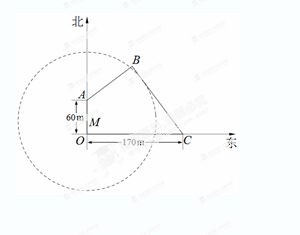
如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80m.经测量,点A位于点O正北方向60m处,点C位于点O正东方向170m处(OC为河岸),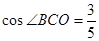 .以
.以 所在直线为
所在直线为 轴,以
轴,以 所在直线为
所在直线为 轴建立平面直角坐标系.
轴建立平面直角坐标系.
(Ⅰ)求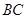 所在直线的方程及新桥BC的长;
所在直线的方程及新桥BC的长;
(Ⅱ)当OM多长时,圆形保护区的面积最大?
并求此时圆的方程.