已知四棱锥P-ABCD,底面是边长为1的正方形,侧棱PC长为2,且PC⊥底面ABCD,E是侧棱PC上的动点。
(Ⅰ)不论点E在何位置,是否都有BD⊥AE?证明你的结论;
(Ⅱ)求点C到平面PDB的距离;
(Ⅲ)若点E为PC的中点,求二面角D-AE-B的大小.
.(本小题满分12分)在右图所示的多面体中,
下部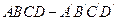 为正方体, 点
为正方体, 点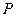 在
在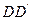 的延长线上,
的延长线上,
且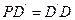 ,
,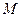 、
、 分别为
分别为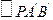 和
和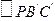 的重心.
的重心.
(1 )已知
)已知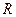 为棱
为棱 上任意一点,求证:
上任意一点,求证: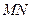 ∥面
∥面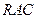 ;
;
(2)求二面角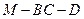 的大
的大 小.
小. 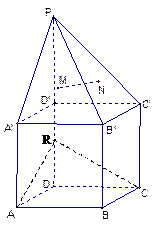
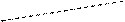 |
.(本小题满分12分)在△ABC中,内角A、B、C所对边的边长分别为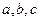 ,
,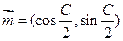 ,
,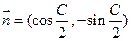 ,且
,且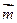 与
与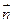 的夹角为
的夹角为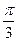 。
。
(1)求内角C;
(2)已知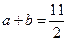 ,且△ABC的面积
,且△ABC的面积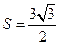 。求
。求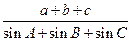 的值。
的值。
.(本小题满分12分)一位客人去北京旅游,他游览长城、故宫、鸟巢这三个景点的概率分别为0.9、0.8、0.8,且他是否游览哪个景点互不影响.设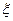 表示客人离开北京时游览的景点数与没有游览的景点数之差的绝对值.
表示客人离开北京时游览的景点数与没有游览的景点数之差的绝对值.
(1)求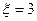 时的概率;
时的概率;
(2)记“函数 在区间
在区间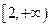 上是增函数”为事件A,求事件A的概率.
上是增函数”为事件A,求事件A的概率.
.(本小题满分12分)已知数列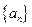 、
、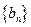 均为等差数列,设
均为等差数列,设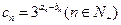 .
.
(1)数列 是否为等比数列?证明你的结论;
是否为等比数列?证明你的结论;
(2)设数列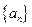 、
、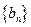 的前n项和分别为
的前n项和分别为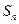 和
和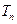 ,若
,若 ,
,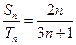 ,
,
求数列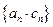 的前n项和 .
的前n项和 .
..已知动圆P过点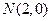 并且与圆
并且与圆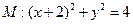 相外切,动圆圆心P的轨迹为W,过点N的直线
相外切,动圆圆心P的轨迹为W,过点N的直线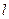 与轨迹W交于A、B两点。
与轨迹W交于A、B两点。
(1)求轨迹W的方程;
(2)若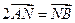 ,求直线
,求直线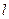 的方程;
的方程;
(3)对于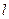 的任意一确定的位置,在直线
的任意一确定的位置,在直线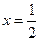 上是否存在一点Q,使得
上是否存在一点Q,使得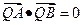 ,并说明理由。
,并说明理由。