如图,在棱长为1的正方体ABCD—A1B1C1D1中,点E是棱BC的中点,点F是棱
CD上的动点.
(I)试确定点F的位置,使得D1E⊥平面AB1F;
(II)当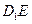 ⊥平面AB1F时,求二面角C1—EF—A的大小(结果用反三角函数值表示).
⊥平面AB1F时,求二面角C1—EF—A的大小(结果用反三角函数值表示).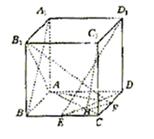
武汉市某地西瓜从2012年6月1日起开始上市。通过市场调查,得到西瓜种植成本Q(单位:元/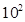 kg)与上市时间t(单位:天)的数据如下表:
kg)与上市时间t(单位:天)的数据如下表:
| 时间t |
50 |
110 |
250 |
| 种植成本Q |
150 |
108 |
150 |
求:1)根据上表数据,从下列函数中选取一个函数描述西瓜种植成本Q与上市时间t的变化关系。
Q=at+b, Q=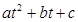 , Q= a
, Q= a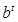 , Q=a
, Q=a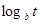 .
.
2)利用你选取的函数,求西瓜种植成本最低时的上市天数及最低种植成本。
已知-1≤x≤2,求函数f(x)=3+2·3x+1-9x的值域.
求值:1)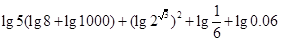 ;
;
2)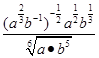
若集合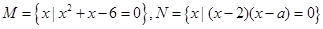 ,且
,且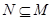 ,求实数
,求实数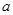 的值;
的值;
本小题满分13分)
已知圆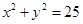 ,△ABC内接于此圆,A点的坐标(3,4),O为坐标原点.
,△ABC内接于此圆,A点的坐标(3,4),O为坐标原点.
(Ⅰ)若△ABC的重心是G(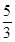 ,2),求BC中点D的坐标及直线BC的方程;
,2),求BC中点D的坐标及直线BC的方程;
(Ⅱ)若直线AB与直线AC的倾斜角互补,求证:直线BC的斜率为定值.