数列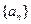 中,
中, 且满足
且满足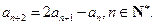
(Ⅰ)求数列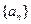 的通项公式;
的通项公式;
(Ⅱ)设 求
求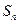 的解析式;
的解析式;
(Ⅲ)设计一个求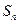 的程序框图.
的程序框图.
(本大题共14分)已知数列 的前n项和
的前n项和 ,且
,且 是
是 与1的等差中项.
与1的等差中项.
(1)求数列 和数列
和数列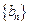 的通项公式;(2)若
的通项公式;(2)若 ,求
,求 ;
;
(3)若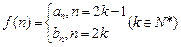 ,是否存在
,是否存在 使得
使得 ,并说明理由.
,并说明理由.
(本大题共14分)已知函数 (
( 为常数),若函数
为常数),若函数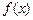 的最大值为
的最大值为 .(1)求实数
.(1)求实数 的值;(2)将函数
的值;(2)将函数 的图象向左平移
的图象向左平移 个单位,再向下平移2个单位得到函数
个单位,再向下平移2个单位得到函数 的图象,求函数
的图象,求函数 的单调递减区间.
的单调递减区间.
已知函数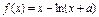 在
在 处取得极值。
处取得极值。
(1)求实数 的值;(2)若关于
的值;(2)若关于 的方程
的方程 在
在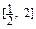 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数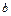 的取值范围;(3)证明:
的取值范围;(3)证明: 。参考数据:
。参考数据: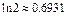 。
。
已知数列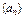 满足
满足 ,且
,且 。
。
(1)证明:数列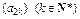 为等比数列;(2)求数列
为等比数列;(2)求数列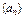 的通项公式;
的通项公式;
(3)设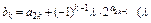 为非零常数)。试确定
为非零常数)。试确定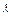 的值,使得对任意
的值,使得对任意 都有
都有 成立。
成立。
已知函数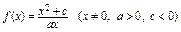 。当
。当 时,函数
时,函数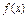 的取值范围恰为
的取值范围恰为 。
。
(1)求函数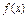 的解析式;(2)若向量
的解析式;(2)若向量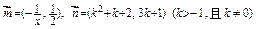 ,解关于
,解关于 的不等式
的不等式 。
。