(本小题满分12分)设数列 的通项公式为
的通项公式为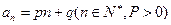 . 数列
. 数列 定义如下:对于正整数m,
定义如下:对于正整数m,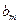 是使得不等式
是使得不等式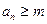 成立的所有n中的最小值.(1)若
成立的所有n中的最小值.(1)若 ,求
,求 ;(2)若
;(2)若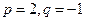 ,求数列
,求数列 的前2m项和公式;(3)是否存在p和q,使得
的前2m项和公式;(3)是否存在p和q,使得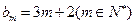 ?如果存在,求p和q的取值范围;如果不存在,请说明理由.
?如果存在,求p和q的取值范围;如果不存在,请说明理由.
设△ABC的内角A,B,C所对的边分别为a,b,c且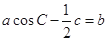 .
.
(Ⅰ)求角A的大小;
(Ⅱ)若a=1,求△ABC的周长的取值范围.
已函数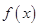 是定义在
是定义在 上的奇函数,在
上的奇函数,在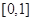 上时
上时
(Ⅰ)求函数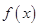 的解析式;
的解析式;
(Ⅱ)解不等式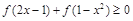 .
.
对于集合M,定义函数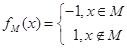 ,对于两个集合M、N,定义集合
,对于两个集合M、N,定义集合 .已知
.已知 ,
, .
.
(Ⅰ)写出 与
与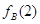 的值,
的值,
(Ⅱ)用列举法写出集合 ;
;
已知函数f(x)=aex,g(x)=lnx-lna,其中a为常数, e=2.718…,且函数y=f(x)和y=g(x)的图像在它们与坐标轴交点处的切线互相平行.
(1)求常数a的值;
(2)若存在x使不等式 >
> 成立,求实数m的取值范围;
成立,求实数m的取值范围;
(3)对于函数y=f(x)和y=g(x)公共定义域内的任意实数x0,我们把|f(x0)-g(x0)|的值称为两函数在x0处的偏差.求证:函数y=f(x)和y=g(x)在其公共定义域内的所有偏差都大于2.
已知函数
(1)若x=2为 的极值点,求实数a的值;
的极值点,求实数a的值;
(2)若 在
在 上为增函数,求实数a的取值范围.
上为增函数,求实数a的取值范围.