(本小题满分13分)如图,已知平行四边形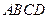 和矩形
和矩形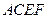 所在的平面互相垂直,
所在的平面互相垂直,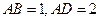 ,
,
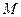 是线段
是线段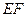 的中点.
的中点.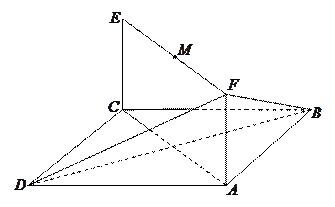
(1)求证: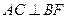 ;(2)求二面角
;(2)求二面角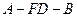 的大小;
的大小;
(3)设点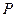 为一动点,若点
为一动点,若点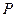 从
从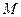 出发,沿棱按照
出发,沿棱按照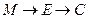
的路线运动到点 ,求这一过程中形成的三棱锥
,求这一过程中形成的三棱锥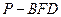 的体积的最小值.
的体积的最小值.
过抛物线C: 上的点M分别向C的准线和x轴作垂线,两条垂线及C的准线和x轴围成边长为4的正方形,点M在第一象限.
上的点M分别向C的准线和x轴作垂线,两条垂线及C的准线和x轴围成边长为4的正方形,点M在第一象限.
(1)求抛物线C的方程及点M的坐标;
(2)过点M作倾斜角互补的两条直线分别与抛物线C交于A,B两点,如果点M在直线AB的上方,求 面积的最大值.
面积的最大值.
商场销售的某种饮品每件售价为36元,成本为20元.对该饮品进行促销:顾客每购买一件,当即连续转动三次如图所示转盘,每次停止后指针向一个数字,若三次指向同一个数字,获一等奖;若三次指向的数字是连号(不考虑顺序),获二等奖;其他情况无奖.
(1)求一顾客一次购买两件该饮品,至少有一件获得奖励的概率;
(2)若奖励为返还现金,一等奖奖金数是二等奖的2倍,统计表明:每天的销售y(件)与一等奖的奖金额x(元)的关系式为 ,问x设定为多少最佳?并说明理由.
,问x设定为多少最佳?并说明理由.
在斜三棱柱 中,平面
中,平面 平面ABC,
平面ABC, ,
, ,
, .
.
(1)求证: ;
;
(2)若 ,求二面角
,求二面角 的余弦值.
的余弦值.
如图,正三角形ABC的边长为2,D,E,F分别在三边AB,BC和CA上,且D为AB的中点, ,
, ,
, .
.
(1)当 时,求
时,求 的大小;
的大小;
(2)求 的面积S的最小值及使得S取最小值时
的面积S的最小值及使得S取最小值时 的值.
的值.
已知函数 ,
, .
.
(1)若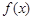 的极大值为
的极大值为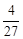 ,求实数
,求实数 的值;
的值;
(2)若对任意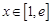 ,都有
,都有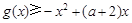 恒成立,求实数
恒成立,求实数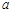 的取值范围;
的取值范围;
(3)若函数f(x)满足:在定义域内存在实数x0,使f(x0+k)= f(x0)+ f(k)(k为常数),则称“f(x)关于k可线性分解”. 设 ,若
,若 关于实数a 可线性分解,求
关于实数a 可线性分解,求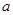 取值范围.
取值范围.