湖北省第十四届运动会纪念章委托某专营店销售，每枚进价5元，同时每销售一枚这种纪念章需向荆州筹委会交特许经营管理费2元，预计这种纪念章以每枚20元的价格销售时该店一年可销售2000枚，经过市场调研发现每枚纪念章的销售价格在每枚20元的基础上每减少一元则增加销售400枚，而每增加一元则减少销售100枚，现设每枚纪念章的销售价格为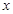
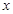元，为整数.
(1)写出该专营店一年内销售这种纪念章所获利润
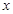(元)与每枚纪念章的销售价格(元)的函数关系式(并写出这个函数的定义域)；
(2)当每枚纪念章销售价格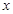为多少元时，该特许专营店一年内利润(元)最大，并求出最大值．
(8分)已知函数
.
（1）写出它的振幅、周期、频率和初相；
（2）求这个函数的单调递减区间；
（3）求出使这个函数取得最大值时，自变量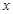
的取值集合，并写出最大值。
（1）化简：
（2）求证：
（本小题满分12分）
已知椭圆
的离心率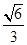为
，右焦点为
。斜率为1的直线
与椭圆
交于
两点，以
为底边作等腰三角形，顶点为
。
（Ⅰ）求椭圆的方程；
（Ⅱ）求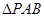
的面积。
（本小题满分12分）
某工厂生产甲、乙两种产品，已知生产每吨甲、乙两种产品所需煤、电力、劳动力、获得利润及每天资源限额（最大供应量）如表所示：
 产品资源 |
甲产品 （每吨） |
乙产品 （每吨） |
资源限额 （每天） |
| 煤（t） |
9 |
4 |
360 |
| 电力（kw·h） |
4 |
5 |
200 |
| 劳力（个） |
3 |
10 |
300 |
| 利润（万元） |
7 |
12 |
问：每天生产甲、乙两种产品各多少吨，获得利润总额最大？
（本小题满分12分）设计一副宣传画，要求画面积为4840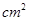
，画面的宽与高的比为
，画面的上，下各留8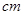
空白，左右各留5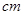空白，怎样确定画面的高于宽尺寸，能使宣传画所用纸张面积最小？