奇瑞公司生产的“奇瑞”轿车是我国民族汽车品牌.该公司2009年生产的“旗云”、“风云”、“ 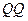 ”三类经济型轿车中,每类轿车均有舒适和标准两种型号.某周产量如下表:
”三类经济型轿车中,每类轿车均有舒适和标准两种型号.某周产量如下表:
| 车型 |
旗云 |
风云 |
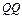 |
| 舒适 |
100 |
150 |
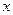 |
| 标准 |
300 |
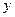 |
600 |
若按分层抽样的方法在这一周生产的轿车中抽取50辆进行检测,则必须抽取“旗云”轿车10辆, “风云”轿车15辆.
(Ⅰ)求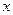 ,
,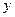 的值;
的值;
(Ⅱ)在年终促销活动中,奖给了某优秀销售公司2辆舒适型和3辆标准型“ 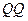 ”轿车,该销售公司又从中随机抽取了2辆作为奖品回馈消费者.求至少有一辆是舒适型轿车的概率;
”轿车,该销售公司又从中随机抽取了2辆作为奖品回馈消费者.求至少有一辆是舒适型轿车的概率;
(Ⅲ)今从“风云”类轿车中抽取6辆,进行能耗等各项指标综合评价,并打分如下:
9.0 9.2 9.5 8.8 9.6 9.7
现从上面6个分值中随机的一个一个地不放回抽取,规定抽到数9.6或9.7,抽取工作即停止.记在抽取到数9.6或9.7所进行抽取的次数为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
设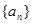 是各项都为正数的等比数列,
是各项都为正数的等比数列,  是等差数列,且
是等差数列,且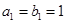 ,
,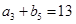 ,
,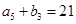 .
.
(1)求数列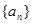 ,
, 的通项公式;
的通项公式;
(2)设数列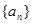 的前
的前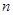 项和为
项和为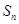 ,求数列
,求数列 的前
的前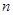 项和
项和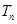 .
.
如图,在底面为平行四边形的四棱柱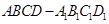 中,
中,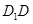
 底面
底面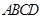 ,
, ,
,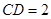 ,
, .
.
(1)求证:平面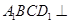 平面
平面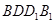 ;
;
(2)若 ,求四棱锥
,求四棱锥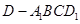 的体积.
的体积.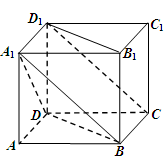
某小组共有 五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)如下表所示:
五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)如下表所示:
| A |
B |
C |
D |
E |
|
| 身高 |
1.69 |
1.73 |
1.75 |
1.79 |
1.82 |
| 体重指标 |
19.2 |
25.1 |
18.5 |
23.3 |
20.9 |
(1)从该小组身高低于1.80的同学中任选2人,求选到的2人身高都在1.78以下的概率;
(2)从该小组同学中任选2人,求选到的2人的身高都在1.70以上且体重指标都在[18.5,23.9)中的概率.
已知平面直角坐标系上的三点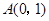 ,
,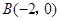 ,
,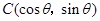 (
(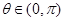 ),
),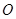 为坐标原点,向量
为坐标原点,向量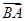 与向量
与向量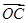 共线.
共线.
(1)求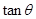 的值;
的值;
(2)求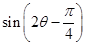 的值.
的值.
设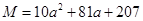 ,
,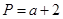 ,Q=
,Q=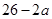 ;若将
;若将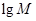 ,lgQ,lgP适当排序后可构成公差为1的等差数列
,lgQ,lgP适当排序后可构成公差为1的等差数列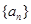 的前三项.
的前三项.
(1)试比较M、P、Q的大小;
(2)求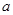 的值及
的值及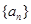 的通项;
的通项;
(3)记函数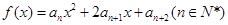 的图象在
的图象在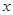 轴上截得的线段长为
轴上截得的线段长为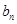 ,
,
设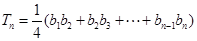
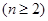 ,求
,求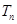 ,并证明
,并证明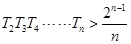 .
.