设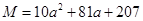 ,
,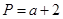 ,Q=
,Q=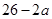 ;若将
;若将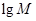 ,lgQ,lgP适当排序后可构成公差为1的等差数列
,lgQ,lgP适当排序后可构成公差为1的等差数列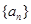 的前三项.
的前三项.
(1)试比较M、P、Q的大小;
(2)求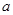 的值及
的值及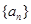 的通项;
的通项;
(3)记函数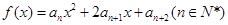 的图象在
的图象在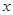 轴上截得的线段长为
轴上截得的线段长为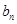 ,
,
设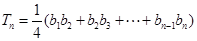
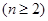 ,求
,求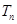 ,并证明
,并证明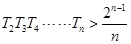 .
.
定义在 上的函数
上的函数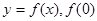
 ,当
,当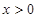 时,
时,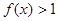 ,且对任意的
,且对任意的 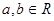 ,有
,有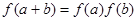 ,
,
(Ⅰ)求证: ;
;
(Ⅱ)求证:对任意的 ,恒有
,恒有 ;
;
(Ⅲ)若 ,求
,求 的取值范围.
的取值范围.
已知函数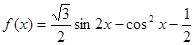 ,
, .
.
(Ⅰ)求函数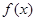 的最小值和最小正周期;
的最小值和最小正周期;
(Ⅱ)设 的内角
的内角 、
、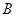 、
、 的对边分别为
的对边分别为 、
、 、
、 ,满足
,满足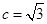 ,
, 且
且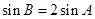 ,求
,求 、
、 的值.
的值.
一个袋中装有大小相同的球10个,其中红球8个,黑球2个,现从袋中有放回地取球,每次随机取1个. 求:
(Ⅰ)连续取两次都是红球的概率;
(Ⅱ)如果取出黑球,则取球终止,否则继续取球,直到取出黑球,取球次数最多不超过4次,求取球次数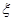 的概率分布列及期望.
的概率分布列及期望.
如图,在四棱锥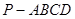 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱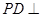 底面ABCD,
底面ABCD, ,E是PC的中点.
,E是PC的中点.
(Ⅰ)证明 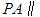 平面EDB;
平面EDB;
(Ⅱ)求EB与底面ABCD所成的角的正切值.
设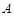 是由
是由 个实数组成的
个实数组成的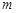 行
行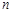 列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.
列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.
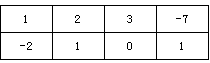
(1)数表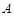 如表1所示,若经过两“操”,使得到的数表每行的各数之和与每列的各数之和均为非负实数,请写出每次“操作”后所得的数表(写出一种方法即可);表1
如表1所示,若经过两“操”,使得到的数表每行的各数之和与每列的各数之和均为非负实数,请写出每次“操作”后所得的数表(写出一种方法即可);表1
| 1 |
2 |
3 |
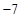 |
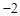 |
1 |
0 |
1 |
(2)数表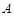 如表2所示,若必须经过两次“操作”,才可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数
如表2所示,若必须经过两次“操作”,才可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数 的所有可能值;表2
的所有可能值;表2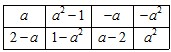
(3)对由 个实数组成的
个实数组成的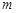 行
行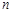 列的任意一个数表
列的任意一个数表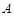 ,能否经过有限次“操作”以后,使得到的数表每行的各数之和与每列的各数之和均为非负实数?请说明理由.
,能否经过有限次“操作”以后,使得到的数表每行的各数之和与每列的各数之和均为非负实数?请说明理由.