(本小题满分13分)
已知函数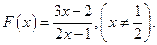
(1)求 ;
;
(2)已知数列 满足
满足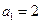 ,
, ,求数列
,求数列 的通项公式;
的通项公式;
(3)求证: .
.
直线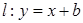 与抛物线
与抛物线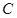
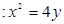 相切于点A.
相切于点A.
(Ⅰ) 求实数 的值,及点A的坐标;
的值,及点A的坐标;
(Ⅱ) 求过点B(0,-1)的抛物线 的切线方程。
的切线方程。
一个计算装置有两个数据输入口Ⅰ、Ⅱ与一个运算结果输出口Ⅲ,当Ⅰ、Ⅱ分别输入正整数 时,输出结果记为
时,输出结果记为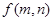 ,且计算装置运算原理如下:①若Ⅰ、Ⅱ分别输入1,则
,且计算装置运算原理如下:①若Ⅰ、Ⅱ分别输入1,则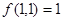 ;②若Ⅰ输入固定的正整数,Ⅱ输入的正整数增大1,则输出结果比原来增大3;③若Ⅱ输入1,Ⅰ输入正整数增大1,则输出结果为原来3倍。
;②若Ⅰ输入固定的正整数,Ⅱ输入的正整数增大1,则输出结果比原来增大3;③若Ⅱ输入1,Ⅰ输入正整数增大1,则输出结果为原来3倍。
试求:(1)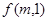 的表达式
的表达式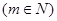 ;
;
(2)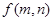 的表达式
的表达式 ;
;
(3)若Ⅰ、Ⅱ都输入正整数 ,则输出结果
,则输出结果 能否为2013?
能否为2013?
若能,求出相应的 ;若不能,则请说明理由。
;若不能,则请说明理由。
已知椭圆C的方程为 ,双曲线
,双曲线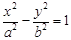 的两条渐近线为
的两条渐近线为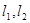 ,过椭圆C的右焦点F作直线
,过椭圆C的右焦点F作直线 ,使
,使 ,又
,又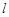 与
与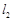 交于P,设
交于P,设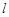 与椭圆C的两个交点由上至下依次为A、B(如图).
与椭圆C的两个交点由上至下依次为A、B(如图).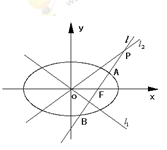
(1)当 与
与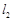 的夹角为
的夹角为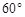 ,且△POF的面积为
,且△POF的面积为 时,求椭圆C的方程;
时,求椭圆C的方程;
(2)当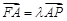 时,求当
时,求当 取到最大值时椭圆的离心率.
取到最大值时椭圆的离心率.
一个四棱锥 的底面是边长为
的底面是边长为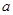 的正方形,侧面展开图如图所示.
的正方形,侧面展开图如图所示. 为四棱锥中最长的侧棱,点
为四棱锥中最长的侧棱,点 为
为 的中点
的中点
(1)画出四棱锥 的示意图,求二面角
的示意图,求二面角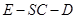 的大小;
的大小;
(2)求点 到平面
到平面 的距离.
的距离.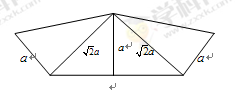
设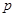 :方程
:方程 有两个不等的负根,
有两个不等的负根,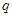 :方程
:方程 无实根,若p或q为真,p且q为假,求
无实根,若p或q为真,p且q为假,求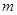 的取值范围.
的取值范围.