某校有在校高中生共1600人,其中高一学生520人,高二学生500人,高三学生580.如果想通过抽查其中的80人,来调查学生的消费情况,考虑到学生的年级高低消费情况有明显差别,而同一年级内消费情况差异较小,问应当采用怎样的抽样方法?高三学生中应抽查多少人?
已知椭圆 长轴上有一顶点到两个焦点之间的距离分别为:3+2
长轴上有一顶点到两个焦点之间的距离分别为:3+2 ,3-2
,3-2 .
.
(1)求椭圆的方程;
(2)如果直线  与椭圆相交于A,B,若C(-3,0),D(3,0),证明:直线CA与直线BD的交点K必在一条确定的双曲线上;
与椭圆相交于A,B,若C(-3,0),D(3,0),证明:直线CA与直线BD的交点K必在一条确定的双曲线上;
(3)过点Q(1,0 )作直线l (与x轴不垂直)与椭圆交于M,N两点,与y轴交于点R,若 ,求证:
,求证: 为定值.
为定值.
设数列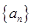 的前
的前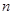 项和为
项和为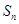 ,已知
,已知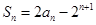 (n∈N*).
(n∈N*).
(1)求数列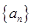 的通项公式;
的通项公式;
(2)设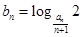 ,数列
,数列 的前
的前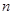 项和为
项和为 ,若存在整数
,若存在整数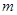 ,使对任意n∈N*且n ≥2,都有
,使对任意n∈N*且n ≥2,都有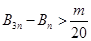 成立,求
成立,求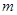 的最大值;
的最大值;
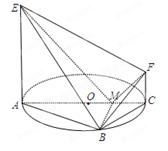
如图,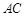 是圆
是圆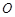 的直径,点
的直径,点 在圆
在圆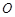 上,
上,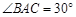 ,
,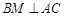 交
交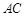 于点
于点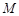 ,
,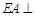 平面
平面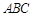 ,
,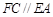 ,
,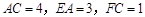 .
.
(1)证明: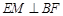 ;
;
(2)求平面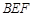 与平面
与平面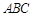 所成的锐二面角的大小.
所成的锐二面角的大小.
已知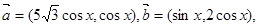 设函数
设函数
(Ⅰ)当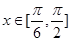 ,求函数
,求函数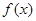 的的值域;
的的值域;
|
(Ⅱ)当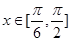 时,若
时,若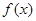 ="8," 求函数
="8," 求函数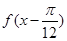 的值;
的值;
已知函数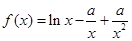 (
(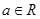 ).
).
(1)若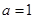 ,求函数
,求函数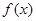 的极值;
的极值;
(2)若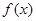 在
在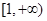 内为单调增函数,求实数a的取值范围;
内为单调增函数,求实数a的取值范围;
(3)对于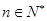 ,求证:
,求证: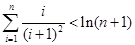 .
.