如图所示:一吊灯的下圆环直径为4m,圆心为O,通过细绳悬挂在天花板上,圆环呈水平状态,并且与天花板的距离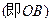 为2m,在圆环上设置三个等分点A1,A2,A3。点C为
为2m,在圆环上设置三个等分点A1,A2,A3。点C为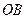 上一点(不包含端点O、B),同时点C与点A1,A2,A3,B均用细绳相连接,且细绳CA1,CA2,CA3的长度相等。设细绳的总长为ym。(1)设∠CA1O =
上一点(不包含端点O、B),同时点C与点A1,A2,A3,B均用细绳相连接,且细绳CA1,CA2,CA3的长度相等。设细绳的总长为ym。(1)设∠CA1O = 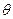 (rad),将y表示成θ的函数关系式;(2)请你设计
(rad),将y表示成θ的函数关系式;(2)请你设计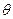 ,当角θ正弦值的大小是多少时,细绳总长y最小,并指明此时 BC应为多长。
,当角θ正弦值的大小是多少时,细绳总长y最小,并指明此时 BC应为多长。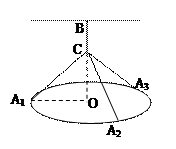
(本小题满分12分)已知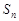 是等差数列
是等差数列 的前
的前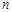 项和,已知
项和,已知 ,且
,且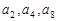 成等比数列
成等比数列
(1)求数列 的通项公式;
的通项公式;
(2)若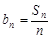 ,求
,求 的值.
的值.
选修4—5:不等式选讲
已知 为正实数,且满足
为正实数,且满足 .
.
(1)求 的最小值;
的最小值;
(2)求证: .
.
选修4-4:极坐标与参数方程
已知曲线C的极坐标方程 是 =1,以极点为原点,极轴为
=1,以极点为原点,极轴为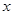 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线 的参数方程为
的参数方程为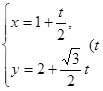 为参数).
为参数).
(1)写出直线 与曲线C的直角坐标方程;
与曲线C的直角坐标方程;
(2)设曲线C经过伸缩变换 得到曲线
得到曲线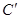 ,设曲线
,设曲线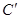 上任一点为
上任一点为 ,求
,求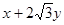 的最小值.
的最小值.
选修4-1:几何证明选讲
如图所示,已知⊙O1与⊙O2相交于A,B两点,过点A作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1,⊙O2于点D,E,DE与AC相交于点P.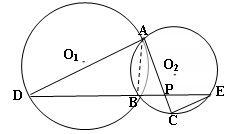
(1)求证:AD∥EC;
(2)若AD是⊙O2的切线,且PA=6,PC=2,BD=9,求AD的长;
设函数 ,其中
,其中 .
.
(Ⅰ)当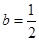 时,判断函数
时,判断函数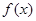 在定义域上的单调性;
在定义域上的单调性;
(Ⅱ)当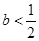 时,求函数
时,求函数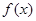 的极值点
的极值点
(Ⅲ)证明:对任意的正整数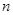 ,不等式
,不等式 都成立.
都成立.