选修4-1:几何证明选讲
如图所示,已知⊙O1与⊙O2相交于A,B两点,过点A作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1,⊙O2于点D,E,DE与AC相交于点P.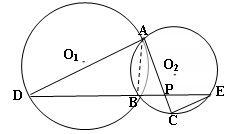
(1)求证:AD∥EC;
(2)若AD是⊙O2的切线,且PA=6,PC=2,BD=9,求AD的长;
(本小题满分12分)
已知p:方程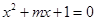 有两个不等的负根;
有两个不等的负根;
q:方程 无实根.若“p或q”为真,“p且q”为假,
无实根.若“p或q”为真,“p且q”为假,
求m的取值范围.
(本小题满分12分)四棱锥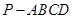 的底面是正方形,
的底面是正方形,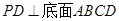 ,点E在棱PB上.若AB=
,点E在棱PB上.若AB=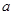 ,
,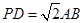
(Ⅰ)求证:平面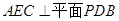 ;
;
(Ⅱ)若E为PB的中点时,求AE与平面PDB所成的角的大小.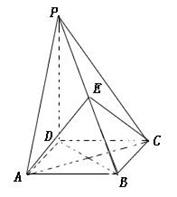
某校从参加高二年级期中考试的学生中抽出60名学生,将其成绩(均为整数)分成六段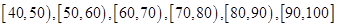 后,画出如下部分频率分布直方图。观察图形,回答下列问题:
后,画出如下部分频率分布直方图。观察图形,回答下列问题:
(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分以上为及格);
(3)估计这次考试的平均分。
(本小题满分12分)
有4张面值相同的债券,其中有2张中奖债券.
(1)有放回地从债券中任取2次,每次取出1张,计算取出的2张都是中奖债券的概率.
(2)无放回地从债券中任取2次,每次取出1张,计算取出的2张中至少有1张是中奖债券的概率.
(本小题满分14分)(注意:仙中、一中、八中的学生三问全做,其他学校的学生只做前两问)
已知函数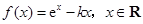
(Ⅰ)若 ,试确定函数
,试确定函数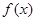 的单调区间;
的单调区间;
(Ⅱ)若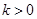 ,且对于任意
,且对于任意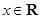 ,
,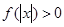 恒成立,试确定实数
恒成立,试确定实数 的取值范围;
的取值范围;
(Ⅲ)设函数 ,求证:
,求证: .
.