(本小题满分12分)
有4张面值相同的债券,其中有2张中奖债券.
(1)有放回地从债券中任取2次,每次取出1张,计算取出的2张都是中奖债券的概率.
(2)无放回地从债券中任取2次,每次取出1张,计算取出的2张中至少有1张是中奖债券的概率.
高二年级的一个研究性学习小组在网上查知,某珍贵植物种子在一定条件下发芽成功的概率为 ,该研究性学习小组又分成两个小组进行验证性实验.
,该研究性学习小组又分成两个小组进行验证性实验.
(1)第1组做了5次这种植物种子的发芽实验(每次均种下一粒种子),求他们的实验至少有3次成功的概率;
(2)第二小组做了若干次发芽试验(每次均种下一粒种子),如果在一次实验中种子发芽成功就停止实验,否则将继续进行下次实验,直到种子发芽成功为止,但发芽实验的次数最多不超过5次,求第二小组所做种子发芽实验的次数 的概率分布列和期望.
的概率分布列和期望.
如图,三棱柱ABC-A1B1C1的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是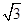 ,D是AC的中点.
,D是AC的中点.
(1)求证:B1C∥平面A1BD;
(2)求二面角A1-BD-A的大小;
(3)求直线AB1与平面A1BD所成的角的正弦值.
若 的展开式中前三项系数成等差数列,
的展开式中前三项系数成等差数列,
求:(1)展开式中含的一次幂的项;
(2)展开式中所有的有理项
(3)展开式中系数最大的项
已知 ,命题
,命题 函数
函数 在
在 上单调递减,命题
上单调递减,命题 曲线
曲线 与
与 轴交于不同的两点,若
轴交于不同的两点,若 为假命题,
为假命题, 为真命题,求实数
为真命题,求实数 的取值范围。
的取值范围。
已知函数 ,
, .
.
(1)若 ,求函数
,求函数 的解析式;
的解析式;
(2)若 时,
时, 的图像与
的图像与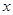 轴有交点,求实数
轴有交点,求实数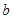 的取值范围.
的取值范围.