如图,椭圆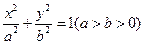 与一等轴双曲线相交,
与一等轴双曲线相交,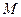 是其中一个交点,并且双曲线的顶点是该椭圆的焦点
是其中一个交点,并且双曲线的顶点是该椭圆的焦点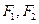 ,双曲线的焦点是椭圆的顶点
,双曲线的焦点是椭圆的顶点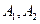 ,
,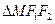 的周长为
的周长为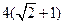 .设
.设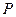 为该双曲线上异于顶点的任一点,直线
为该双曲线上异于顶点的任一点,直线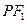 和
和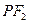 与椭圆的交点分别为
与椭圆的交点分别为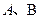 和
和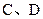 .
.
(Ⅰ)求椭圆和双曲线的标准方程;
(Ⅱ)设直线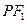 、
、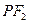 的斜率分别为
的斜率分别为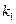 、
、 ,证明
,证明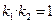 ;
;
(Ⅲ)是否存在常数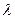 ,使得
,使得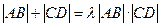 恒成立?若存在,求
恒成立?若存在,求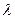 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.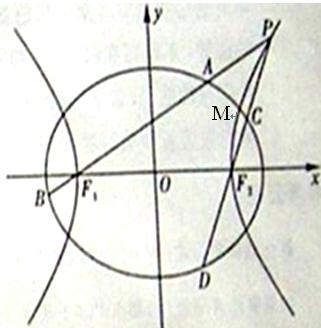
已知函数 ,
, 为常数.
为常数.
(1)若函数 在
在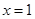 处的切线与
处的切线与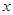 轴平行,求
轴平行,求 的值;
的值;
(2)当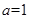 时,试比较
时,试比较 与
与 的大小;
的大小;
(3)若函数 有两个零点
有两个零点 、
、 ,试证明
,试证明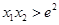 .
.
已知椭圆 的右准线
的右准线 ,离心率
,离心率 ,
,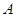 ,
,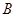 是椭圆上的两动点,动点
是椭圆上的两动点,动点 满足
满足 ,(其中
,(其中 为常数).
为常数).
(1)求椭圆标准方程;
(2)当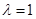 且直线
且直线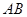 与
与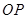 斜率均存在时,求
斜率均存在时,求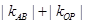 的最小值;
的最小值;
(3)若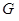 是线段
是线段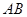 的中点,且
的中点,且 ,问是否存在常数
,问是否存在常数 和平面内两定点
和平面内两定点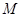 ,
,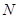 ,使得动点
,使得动点 满足
满足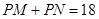 ,若存在,求出
,若存在,求出 的值和定点
的值和定点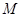 ,
,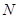 ;若不存在,请说明理由.
;若不存在,请说明理由.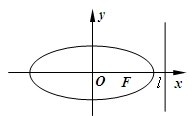
图1是某斜拉式大桥图片,为了了解桥的一些结构情况,学校数学兴趣小组将大桥的结构进行了简化,取其部分可抽象成图2所示的模型,其中桥塔 、
、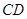 与桥面
与桥面 垂直,通过测量得知
垂直,通过测量得知 ,
,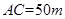 ,当
,当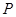 为
为 中点时,
中点时,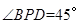 .
.
(1)求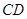 的长;
的长;
(2)试问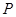 在线段
在线段 的何处时,
的何处时,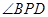 达到最大.
达到最大.
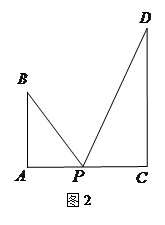
|
如图,四棱锥 中,
中,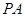 ⊥底面
⊥底面 ,底面
,底面 为菱形,点
为菱形,点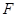 为侧棱
为侧棱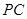 上一点.
上一点.
(1)若 ,求证:
,求证: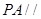 平面
平面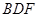 ;
;
(2)若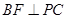 ,求证:平面
,求证:平面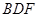 ⊥平面
⊥平面 .
.
在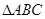 中,角
中,角 ,
, ,
,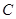 的对边分别为
的对边分别为 ,
,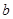 ,
,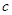 ,若
,若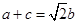 .
.
(1)求证: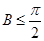 ;
;
(2)当 ,
, 时,求
时,求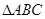 的面积.
的面积.