已知数列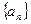 中,
中,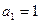 ,
,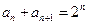 (n∈N*),
(n∈N*),
(1)试证数列 是等比数列,并求数列{
是等比数列,并求数列{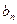 }的通项公式;
}的通项公式;
(2)在数列{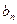 }中,求出所有连续三项成等差数列的项;
}中,求出所有连续三项成等差数列的项;
(3)在数列{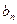 }中,是否存在满足条件1<r<s的正整数r ,s ,使得b1,br,bs成等差数列?若存在,确定正整数r,s之间的关系;若不存在,说明理由.
}中,是否存在满足条件1<r<s的正整数r ,s ,使得b1,br,bs成等差数列?若存在,确定正整数r,s之间的关系;若不存在,说明理由.
已知 、
、 分别是椭圆
分别是椭圆 的左、右焦点,点B是其上顶点,椭圆的右准线与
的左、右焦点,点B是其上顶点,椭圆的右准线与
 轴交于点N,且
轴交于点N,且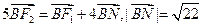 。
。
(1)求椭圆方程;
(2)直线 :
: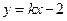 与椭圆交于不同的两点M、Q,若△BMQ是以MQ为底边的等腰三角形,求
与椭圆交于不同的两点M、Q,若△BMQ是以MQ为底边的等腰三角形,求 的值。
的值。
学校欲在操场边上一直角三角形空地ABC上种植草坪,并需铺设一根水管EF(E在AC上,F在AB上)用于灌溉,已知∠A=30°,∠C=90°,BC=2a ,D是BC中点,为确保灌溉的效果,铺设时要求∠EDF=
,D是BC中点,为确保灌溉的效果,铺设时要求∠EDF= 60°。现有两种方案可供参考。甲方案:取AC的中点E铺设水管;乙方案:取AB的中点F铺设水管。
60°。现有两种方案可供参考。甲方案:取AC的中点E铺设水管;乙方案:取AB的中点F铺设水管。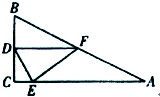
(1)比较甲乙两种方案,哪一种方案更合理(EF的长较小的合理);
(2)学校研究小组通过研究得出:无论D在BC的什么位置,总存在E,F两点,使△DEF为正三角形 。试证明该结论的正确性。
。试证明该结论的正确性。
在四棱锥 中,底面ABCD是矩形,PA=AD=4,AB=2,PB=
中,底面ABCD是矩形,PA=AD=4,AB=2,PB=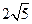 ,PD=
,PD=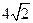 。E是PD的中点。
。E是PD的中点。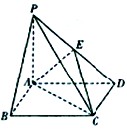
(1)求证:AE⊥平面PCD;
(2)求二面角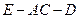 的平面角的大小的余弦值;
的平面角的大小的余弦值;
(3)在线段BC上是否存在点F,使得三棱锥F—ACE的体积恰为 ,
,
若存在,试确定点F的位置;若不存在,请说明理由。
为庆贺2011建党90周年,某机构举办有奖猜奖活动,参与者需先后回答两道选择题:问题A有四个选项,问题B有五个选项,但都只有一个选项是正确的,正确回答问题A可获 得价值
得价值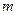 元的礼品,正确回答问题B可获得价值
元的礼品,正确回答问题B可获得价值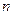 元的礼品,活动规定:参与者可任意选择回答问题的顺序:如果第一个问题回答错误,则该参与者猜奖活动中止,假设参与者在回答问题前,对这两个问题都很陌生,因而准备靠随机猜测回答问题,试确定回答问题的顺序使获得的礼品的价值的期望值较大。
元的礼品,活动规定:参与者可任意选择回答问题的顺序:如果第一个问题回答错误,则该参与者猜奖活动中止,假设参与者在回答问题前,对这两个问题都很陌生,因而准备靠随机猜测回答问题,试确定回答问题的顺序使获得的礼品的价值的期望值较大。
(本小题满分12分)
设 是函数
是函数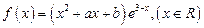 的一个极值点.
的一个极值点.
(1)求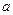 与
与 的关系式(用
的关系式(用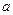 表示
表示 ),并求
),并求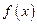 的单调区间;
的单调区间;
(2)设 ,若存在
,若存在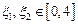 ,使得
,使得 成立,求
成立,求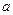 的取值范围.
的取值范围.