在四棱锥
中，底面ABCD是矩形，PA=AD=4，AB=2，PB=
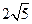，PD=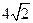
。E是PD的中点。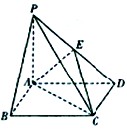
（1）求证：AE⊥平面PCD；
（2）求二面角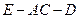
的平面角的大小的余弦值；
（3）在线段BC上是否存在点F，使得三棱锥F—ACE的体积恰为
，
若存在，试确定点F的位置；若不存在，请说明理由。
海关对同时从A，B，C三个不同地区进口的某种商品进行抽样检测，从各地区进口此种商品的数量（单位：件）如下表所示. 工作人员用分层抽样的方法从这些商品中共抽取6件样品进行检测.
| 地区 |
A |
B |
C |
| 数量 |
50 |
150 |
100 |
（Ⅰ）求这6件样品中来自A，B，C各地区商品的数量；
（Ⅱ）若在这6件样品中随机抽取2件送往甲机构进行进一步检测，求这2件商品来自相同地区的概率.
（本小题满分13分）已知函数
.
（1）当
时，求
在
处的切线方程；
（2）设函数
，
（ⅰ）若函数
有且仅有一个零点时，求
的值；
（ⅱ）在（ⅰ）的条件下，若
，
，求
的取值范围．
（本小题满分13分）如图，焦点在x轴的椭圆C：
（b > 0），点G（2，0），点P在椭圆上，且PG⊥x轴，连接OP交直线x = 4于点M，连接MG交椭圆于A、B.
（Ⅰ）若G为椭圆右焦点，求|OM|；
（Ⅱ）记直线PA，PB的斜率分别为
，
，求
的取值范围.
（本小题满分13分）已知数列
中，
，
，记
为的前
项的和．设
，
（1）证明：数列
是等比数列；
（2）不等式：
对于一切
恒成立，求实数
的最大值.
（本小题满分12分）某公司举办一次募捐爱心演出，有1000人参加，每人一张门票，每张100元。在演出过程中穿插抽奖活动，第一轮抽奖从这1000张票根中随机抽取10张，其持有者获得价值1000元的奖品，并参加第二轮抽奖活动。第二轮抽奖由第一轮获奖者独立操作按钮，电脑随机产生两个实数
（
），若满足
，电脑显示“中奖”，则抽奖者再次获得特等奖奖金；否则电脑显示“谢谢”，则不中特等奖奖金。
（Ⅰ）已知小明在第一轮抽奖中被抽中，求小明在第二轮抽奖中获奖的概率；
（Ⅱ）设特等奖奖金为a元，求小李参加此次活动收益的期望，若该公司在此次活动中收益的期望值是至少获利70000元，求a的最大值。