已知9个外语教师，4人只会英语，3人只会日语，另外2人既会英语又会日语，从中选4人，2人教英语，2人教日语，有多少种不同安排方案？（本题12分）
设在海拔
m处的大气压强是
Pa，与之间的函数关系式是
，其中
，
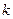为常量．测得某地某天海平面的大气压强为
Pa，1000m高空的大气压为
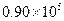Pa，求600m高空的大气压强（保留
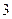个有效数字）．
某商店经销某种洗衣粉，年销售总量为6000包，每包进价2.8元，销售价3.4元．全年分若干次进货，每次进货均为
包．已知每次进货运输劳务费为62.5元，全年保管费为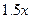
元．求：
（１）把该商店经销洗衣粉一年的利润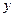
元表示为每次进货量包的函数，并指
出这个函数的定义域．
（２）为了使利润最大，每次应该进货多少包？
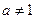
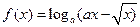
（1）求函数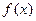
的定义域；
（2）当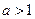
时，判断函数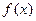的单调性，并用函数单调性的定义证明你的结论
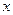
（1）分别写出按甲、乙两种优惠方案实际付款金额
甲（元）、乙（元）与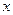之间的函数关系式；
（2）如果该商场即允许只选择一种优惠方案购买，也允许同时用两种优惠方案购买，请你就购买这种毛笔10支和这种书法练习本60本设计一种最省钱的购买方案
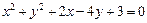
（1）若不经过坐标原点的直线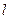
与圆C相切，且直线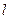在两坐标轴上的截距相等，求直线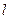的方程；
（2）设点P在圆C上，求点P到直线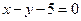
距离的最大值与最小值