如图,在三棱锥 中,
中, 底面
底面 ,点
,点 ,
,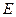 分别在棱
分别在棱 上,且
上,且 (Ⅰ)求证:
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)当 为
为 的中点时,求
的中点时,求 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(Ⅲ)是否存在点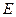 使得二面角
使得二面角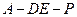 为直二面角?并说明理由.
为直二面角?并说明理由.
设函数f(x)=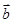 ×
×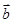 ,其中向量
,其中向量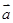 ="(2cosx,1),"
="(2cosx,1)," 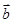 =(cosx,
=(cosx,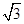 sin2x+m).
sin2x+m).
(1)求函数f(x)的最小正周期和f(x)在[0, p]上的单调递增区间;
(2)当xÎ[0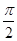 ]时,ô f(x)ô <4恒成立,求实数m的取值范围.
]时,ô f(x)ô <4恒成立,求实数m的取值范围.
已知向量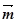 =(sinA,cosA),
=(sinA,cosA),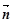 =
=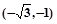 ,
,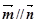 ,且A为锐角.
,且A为锐角.
(1)求角A的大小;
(2)求函数f(x)=cos2x+4cosAsinx,(xÎR) 最大值及取最大值时x的集合.
随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如下图.
(1)根据茎叶图判断哪个班的平均身高较高;
(2)现从乙班这10名同学中随机抽取两名身高不低于173 cm的同学,求身高为176 cm的同学被抽中的概率.
已知函数f(x)是定义在R上的奇函数,并且当x∈(0,+∞)时,f(x)=2x.
(1)求f(log2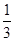 )的值;
)的值;
(2)求f(x)的解析式.
已知f(α)= 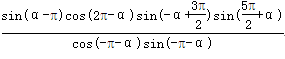
(1)化简f(α)
(2)若cos(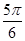 +2α)=
+2α)=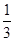 ,求f(
,求f(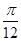 -α)的值.
-α)的值.