已知等差数列{an}的前n项和为Sn,a1=1+,S3=9+3
(1)求数列{an}的通项an与 前n项和Sn;
前n项和Sn;
(2)设 ,求证:数列{bn}中任意不同的三项都不可能成为等比数列.
,求证:数列{bn}中任意不同的三项都不可能成为等比数列.
已知 ,数列
,数列 满足
满足 ,数列
,数列 满足
满足 ;数列
;数列 为公比大于
为公比大于 的等比数列,且
的等比数列,且 为方程
为方程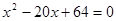 的两个不相等的实根.
的两个不相等的实根.
(Ⅰ)求数列 和数列
和数列 的通项公式;
的通项公式;
(Ⅱ)将数列 中的第
中的第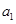 项,第
项,第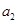 项,第
项,第 项,……,第
项,……,第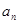 项,……删去后剩余的项按从小到大的顺序排成新数列
项,……删去后剩余的项按从小到大的顺序排成新数列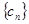 ,求数列
,求数列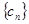 的前
的前 项和.
项和.
如图,几何体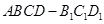 中,四边形
中,四边形 为菱形,
为菱形, ,
, ,面
,面 ∥面
∥面 ,
, 、
、 、
、 都垂直于面
都垂直于面 ,且
,且 ,
, 为
为 的中点.
的中点.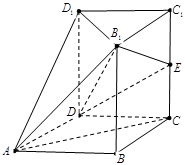
(Ⅰ)求证: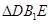 为等腰直角三角形;
为等腰直角三角形;
(Ⅱ)求证: ∥面
∥面 .
.
从某学校的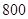 名男生中随机抽取
名男生中随机抽取 名测量身高,被测学生身高全部介于
名测量身高,被测学生身高全部介于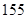 cm和
cm和 cm之间,将测量结果按如下方式分成八组:第一组[
cm之间,将测量结果按如下方式分成八组:第一组[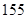 ,
,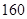 ),第二组[
),第二组[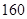 ,
,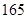 ),…,第八组[
),…,第八组[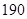 ,
, ],右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为
],右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为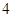 人.
人.
(Ⅰ)求第七组的频率;
(Ⅱ)估计该校的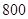 名男生的身高的中位数以及身高在
名男生的身高的中位数以及身高在 cm以上(含
cm以上(含 cm)的人数;
cm)的人数;
(Ⅲ)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为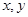 ,事件
,事件 {
{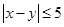 },事件
},事件 {
{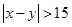 },求
},求 .
.
已知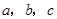 为
为 的内角
的内角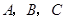 的对边,满足
的对边,满足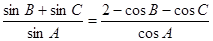 ,函数
,函数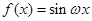
 在区间
在区间 上单调递增,在区间
上单调递增,在区间 上单调递减.
上单调递减.
(Ⅰ)证明: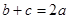 ;
;
(Ⅱ)若 ,证明
,证明 为等边三角形.
为等边三角形.
设函数 ,其中
,其中 为常数.
为常数.
(Ⅰ)当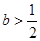 时,判断函数
时,判断函数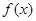 在定义域上的单调性;
在定义域上的单调性;
(Ⅱ)当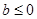 时,求
时,求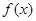 的极值点并判断是极大值还是极小值;
的极值点并判断是极大值还是极小值;
(Ⅲ)求证对任意不小于3的正整数 ,不等式
,不等式 都成立.
都成立.