(本小题满分一10分)【选修4一5:不等式选讲】
已知
(1)求不等式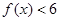 的解集;
的解集;
(2)设m,n,p为正实数,且 ,求证:
,求证: .
.
已知三次函数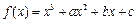 在
在 和
和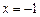 时取极值,且
时取极值,且 .
.
(Ⅰ) 求函数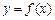 的表达式;
的表达式;
(Ⅱ)求函数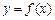 的单调区间和极值;
的单调区间和极值;
(Ⅲ)若函数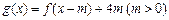 在区间
在区间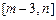 上的值域为
上的值域为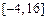 ,试求
,试求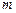 、n应满足的条件。
、n应满足的条件。
设 是平面上的两个向量,且
是平面上的两个向量,且 互相垂直.
互相垂直.
(1)求λ的值;
(2)若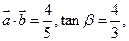 求
求 的值.
的值.
已知数集
具有性质
;对任意的
,
与
两数中至少有一个属于
。
(Ⅰ)分别判断数集
与
是否具有性质
,并说明理由;
(Ⅱ)证明:
,且
;
(Ⅲ)证明:当
时,
成等比数列。
如图,设抛物线方程为x2=2py(p>0),M为直线y=-2p上任意一点,过M引抛物线的切线,切点分别为A,B.
(Ⅰ)求证:A,M,B三点的横坐标成等差数列;
(Ⅱ)已知当M点的坐标为(2,-2p)时, ,求此时抛物线的方程;
,求此时抛物线的方程;
(Ⅲ)是否存在点M,使得点C关于直线AB的对称点D在抛物线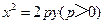 上,其中,点C满足
上,其中,点C满足 (O为坐标原点).若存在,求出所有适合题意的点M的坐标;若不存在,请说明理由.
(O为坐标原点).若存在,求出所有适合题意的点M的坐标;若不存在,请说明理由.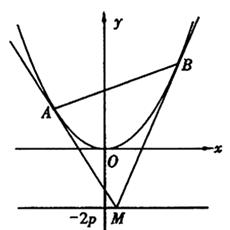
在 平面上有一系列点
平面上有一系列点
 对每个自然数
对每个自然数 ,点
,点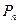 位于函数
位于函数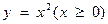 的图象上.以点
的图象上.以点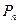 为圆心的⊙
为圆心的⊙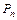 与
与 轴都相切,且⊙
轴都相切,且⊙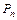 与⊙
与⊙ 又彼此外切.若
又彼此外切.若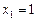 ,且
,且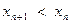
 .
.
(1)求证:数列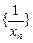 是等差数列;
是等差数列;
(2)设⊙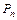 的面积为
的面积为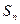 ,
,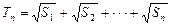 , 求证:
, 求证: