已知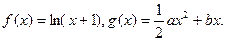
(1)若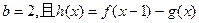 存在单调递减区间,求
存在单调递减区间,求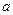 的取值范围;
的取值范围;
(2)若 时,求证
时,求证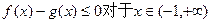 成立;
成立;
(3)利用(2)的结论证明:若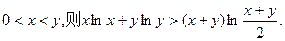
已知椭圆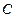 :
: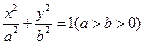 的两个焦点为
的两个焦点为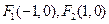 ,点
,点 在椭圆
在椭圆 上.(Ⅰ)求椭圆
上.(Ⅰ)求椭圆 的方程;(Ⅱ)记
的方程;(Ⅱ)记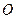 为坐标原点,过
为坐标原点,过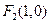 的直线
的直线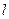 与椭圆
与椭圆 相交于
相交于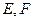 两点,若
两点,若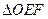 的面积为
的面积为 ,求直线
,求直线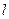 的方程.
的方程.
已知双曲线 的中心在坐标原点
的中心在坐标原点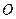 ,对称轴为坐标轴,点
,对称轴为坐标轴,点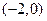 是它的一个焦点,并且离心率为
是它的一个焦点,并且离心率为 .(Ⅰ)求双曲线C的方程;(Ⅱ)已知点
.(Ⅰ)求双曲线C的方程;(Ⅱ)已知点 ,设
,设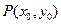 是双曲线
是双曲线 上的点,
上的点,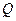 是点
是点 关于原点的对称点,求
关于原点的对称点,求 的取值范围.
的取值范围.
已知直线 为曲线
为曲线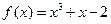 在点
在点 处的切线,直线
处的切线,直线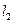 为该曲线的另一条切线,且
为该曲线的另一条切线,且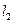 的斜率为1.(Ⅰ)求直线
的斜率为1.(Ⅰ)求直线 、
、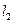 的方程;(Ⅱ)求由直线
的方程;(Ⅱ)求由直线 、
、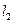 和
和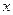 轴所围成的三角形的面积.
轴所围成的三角形的面积.
已知抛物线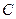 :
: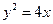 的焦点为
的焦点为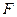 ,直线
,直线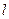 过点
过点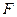 且其倾斜角为
且其倾斜角为 ,设直线
,设直线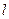 与曲线
与曲线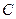 相交于
相交于 、
、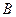 两点,求以线段
两点,求以线段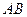 为直径的圆的标准方程.
为直径的圆的标准方程.
袋中有2个红球,3个白球,摸出一个红球得5分,摸出一个白球得3分,现从中任意摸出2个球,求事件“所得分数不小于8分”的概率.