已知函数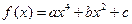 的图象过点
的图象过点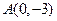 ,且它在
,且它在 处的切线方程为
处的切线方程为 .
.
(1) 求函数 的解析式;
的解析式;
(2) 若对任意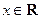 ,不等式
,不等式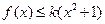 恒成立,求实数
恒成立,求实数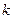 的取值范围.
的取值范围.
已知 是实数,函数
是实数,函数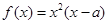 。
。
(Ⅰ)若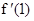 =3,求
=3,求 的值及曲线
的值及曲线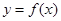 在点
在点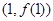 处的切线方程;
处的切线方程;
(Ⅱ)求 在区间
在区间 上的最大值。
上的最大值。
如图,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2),A(x1,y1),B(x2,y2)均在抛物线上.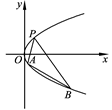
(1)写出该抛物线的标准方程及其准线方程;
(2)当直线 与
与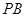 的斜率存在且倾斜角互补时,求
的斜率存在且倾斜角互补时,求 的值及直线
的值及直线 的斜率.
的斜率.
设函数 ,曲线
,曲线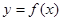 过P(1,0),且在P点处的切斜线率为2.
过P(1,0),且在P点处的切斜线率为2.
(I)求a,b的值;(II)令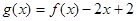 ,求
,求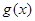 的单调区间.
的单调区间.
某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段: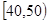 ,
,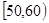 ,…,
,…, 后得到如图的频率分布直方图.
后得到如图的频率分布直方图.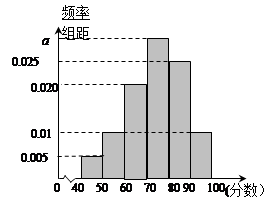
(1)求图中实数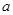 的值;
的值;
(2)若该校高一年级共有学生640人,试估计该校高一年级.期中考试数学成绩不低于60分的人数;
现有6道题,其中4道甲类题,2道乙类题,张同学从中任取2道题解答.试求:
(Ⅰ)所取的2道题都是甲类题的概率;
(Ⅱ)所取的2道题不是同一类题的概率.