已知关于 的函数 ,其导函数为 。令 ,记函数 在区间[-1、1]上的最大值为 .
(Ⅰ)如果函数
在
处有极值-
,试确定
的值;
(Ⅱ)若
,证明对任意的
,都有
;
(Ⅲ)若
对任意的
恒成立,试求
的最大值。
(本小题12分)已知函数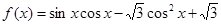 ,
, 。
。
(1)求函数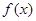 的最大值和单调递减区间;
的最大值和单调递减区间;
(2)已知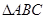 的内角
的内角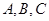 的对边分别为
的对边分别为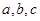 ,设角
,设角 是
是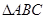 的最大角,且
的最大角,且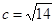 ,
,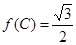 .若向量
.若向量 与向量
与向量 垂直,求
垂直,求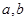 的值。
的值。
(本小题12分)化简下列各式:(1)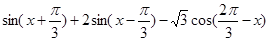 ;
;
(2)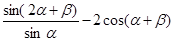 。
。
(本小题满分14分)已知抛物线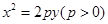 ,直线
,直线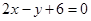 截抛物线C所得弦长为
截抛物线C所得弦长为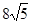 .
.
(1)求抛物线的方程;
(2)已知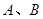 是抛物线上异于原点
是抛物线上异于原点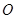 的两个动点,记
的两个动点,记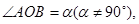 若
若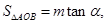 试求当
试求当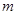 取得最小值时
取得最小值时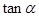 的最大值.
的最大值.
(本小题满分13分)已知函数 在
在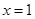 处取得极小值.
处取得极小值.
(1)求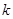 的值;
的值;
(2)若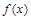 在
在 处的切线方程为
处的切线方程为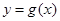 ,求证:当
,求证:当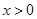 时,曲线
时,曲线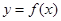 不可能在直线
不可能在直线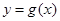 的下方.
的下方.
(本小题满分12分)已知等比数列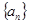 的首项
的首项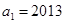 ,公比
,公比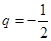 ,数列
,数列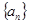 前
前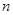 项的积记为
项的积记为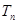 .
.
(1)求使得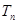 取得最大值时
取得最大值时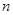 的值;
的值;
(2)证明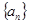 中的任意相邻三项按从小到大排列,总可以使其成等差数列,如果所有这些等差数列的公差按从小到大的顺序依次设为
中的任意相邻三项按从小到大排列,总可以使其成等差数列,如果所有这些等差数列的公差按从小到大的顺序依次设为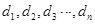 ,证明:数列
,证明:数列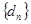 为等比数列.(参考数据
为等比数列.(参考数据 )
)