(本题满分13分)如图,棱柱ABCD—A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1C1C⊥平面ABCD,∠A1AC=60°. (Ⅰ)证明:BD⊥AA1;
(Ⅱ)求二面角D—A1A—C的平面角的余弦值; (Ⅲ)在直线CC1上是否存在点P,使BP//平面DA1C1?若存在,求出点P的位置;若不存在,说明理由.
设函数 ,
,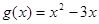 ,记
,记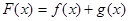
(1)求曲线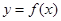 在
在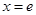 处的切线方程;
处的切线方程;
(2)求函数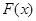 在
在 上的最值.
上的最值.
扶余市为“市中学生知识竞赛”进行选拔性测试,且规定:成绩大于或等于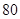 分的有参赛资格,
分的有参赛资格,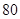 分以下(不包括
分以下(不包括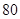 分)的则被淘汰。若现有
分)的则被淘汰。若现有 人参加测试,学生成绩的频率分布直方图如下:
人参加测试,学生成绩的频率分布直方图如下: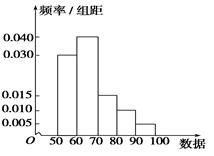
(1)求获得参赛资格的人数;
(2)根据频率分布直方图,估算这 名学生测试的平均成绩.
名学生测试的平均成绩.
(本小题满分14分)已知圆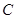 经过点A(-2,0),B(0,2),且圆心
经过点A(-2,0),B(0,2),且圆心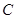 在直线y=x上,又直线l:y=kx+1与圆
在直线y=x上,又直线l:y=kx+1与圆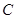 相交于P、Q两点.
相交于P、Q两点.
(1)求圆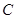 的方程;
的方程;
(2)若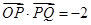 ,求实数k的值;
,求实数k的值;
(3)过点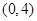 作动直线
作动直线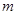 交圆
交圆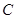 于
于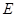 ,
,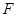 两点.试问:在以
两点.试问:在以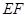 为直径的所有圆中,是否存在这样的圆
为直径的所有圆中,是否存在这样的圆 ,使得圆
,使得圆 经过点
经过点 ?若存在,求出圆
?若存在,求出圆 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(本小题满分13分)受轿车在保修期内维修费等因素的影响,企业生产每辆轿车的利润与该轿车首次出现故障的时间有关,某轿车制造厂生产甲、乙两种品牌轿车,保修期均为2年,现从该厂已售出的两种品牌轿车中随机抽取50辆,统计数据如下:
| 品牌 |
甲 |
乙 |
|||
首次出现故障时间 年 年 |
 |
 |
 |
 |
 |
| 轿车数量(辆) |
2 |
3 |
45 |
5 |
45 |
| 每辆利润(万元) |
1 |
2 |
3 |
 |
 |
将频率视为概率,解答下列问题:
(1)从该厂生产的甲品牌轿车中随机抽取一辆,求首次出现故障发生在保修期内的概率;
(2)若该厂生产的轿车均能售出,记生产一辆甲品牌轿车的利润为 ,生产一辆乙品牌轿车的利润为
,生产一辆乙品牌轿车的利润为 ,分别求
,分别求 的分布列;
的分布列;
(3)该厂预计今后这两种品牌轿车销量相当,由于资金限制,只能生产其中一种品牌轿车,若从生产一辆品牌轿车的利润均值的角度考虑,你认为应该生产哪种品牌的轿车?说明理由.
(本小题满分12分)已知关于 的一元二次函数
的一元二次函数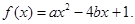
(1)若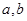 分别表示将一枚质地均匀的骰子先后抛掷两次时第一次、第二次正面朝上出现的点数,求满足函数
分别表示将一枚质地均匀的骰子先后抛掷两次时第一次、第二次正面朝上出现的点数,求满足函数 在区间[
在区间[ 上是增函数的概率;
上是增函数的概率;
(2)设点( ,
,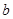 )是区域
)是区域 内的随机点,求函数
内的随机点,求函数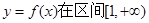 上是增函数的概率.
上是增函数的概率.