（本小题满分12分）
的内切圆与三边AB、BC、CA的切点分别为D、E、F，已知
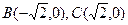，内切圆圆心
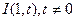，设点A的轨迹为L。 （1）求L的方程；
（2）过点C的动直线
交曲线L于不同的两点M、N，问在
轴上是否存在一定点Q（Q不与C重合），使
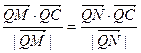恒成立，若存在，试求出Q点的坐标，若不存在，说明理由。
在长方体ABCD-A1B1C1D1中,AB=3,AD=2,CC1=1,一条绳子从点A沿表面拉到点C1,求绳子的最短的长. 
边长为5的正方形EFGH是圆柱的轴截面,求从点E沿圆柱的侧面到相对顶点G的最短距离.
判断下列各句话的对错.
(1)有两个面平行,其余各面都是平行四边形的几何体是棱柱.
(2)一个棱柱至少有五个面.
(3)用一个平面去截棱锥,底面和截面之间的部分叫棱台.
(4)棱台的各侧棱延长后交于一点.
(5)棱台的侧面是等腰梯形.
(6)以直角梯形的一腰为旋转轴,另一腰为母线的旋转面是圆台的侧面.
如图所示为长方体ABCD-A′B′C′D′,当用平面BCFE把这个长方体分成两部分后,各部分形成的多面体还是棱柱吗？如果不是,请说明理由;若是,指出底面及侧棱. 
已知集合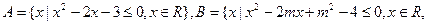
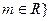
（1）若
，求实数m的值；
（2）若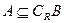
，求实数m的取值范围.