如图,⊙O是等腰三角形ABC的外接圆,AB=AC,延长BC到点D,使CD=AC,连接AD交⊙O于点E,连接BE与AC交于点F.
⑴判断BE是否平分∠ABC,并说明理由;
⑵若AE=6,BE=8,求EF的长.
(本小题10分)如图,在三棱锥P-ABC中, 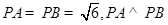 ,
, ,平面PAB
,平面PAB  平面ABC.
平面ABC.
(1)求证:PA  BC:
BC:
(2)求PC的长度;
(3)求二面角P-AC-B的正切值
(本小题8分)已知点P(-4,0)及圆C:
(1)当直线  过点P且与圆心C的距离为l时,求直线
过点P且与圆心C的距离为l时,求直线  的方程:
的方程:
(2)设过点P的直线与圆C交于A、B两点,当  取得最小值时,求以线段AB为直径的圆的方程,
取得最小值时,求以线段AB为直径的圆的方程,
(本小题8分)如图,在直三棱柱 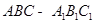 中,AB=AC,D、E分别是棱BC、
中,AB=AC,D、E分别是棱BC、  上的点(点D不在BC的端点处),且AD
上的点(点D不在BC的端点处),且AD DE,F为
DE,F为  的中点.
的中点.
(1)求证:平面ADE 平面
平面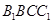 ;
;
(2)求证: 平面ADE.
平面ADE.
(本小题8分)根据下列条件写出直线的方程,并且化成—般式
(1)经过点 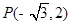 且倾斜角
且倾斜角 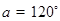 ;
;
(2)经过点A(-1,0)和B(2,-3).
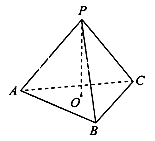
(本小题6分)如图,已知—正三棱锥P- ABC的底面棱长AB=3,高PO= 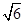 ,求这个正三棱锥的表面积.
,求这个正三棱锥的表面积.