为了让学生了解更多“社会法律”知识,
| 分组 |
频数 |
频率 |
| 60.5~70.5 |
1 |
0.16 |
| 70.5~80.5 |
10 |
2 |
| 80.5~90.5 |
18 |
0.36 |
| 90.5~100.5 |
3 |
4 |
| 合计 |
50 |
1 |
某中学举行了一次“社会法律知识竞赛”,
共有800名学生参加了这次竞赛. 为了解
本次竞赛成绩情况,从中抽取了部分学
生的成绩(得分均为整数,满分为100
分)进行统计.请你根据尚未完成并有
局部污损的频率分布表,解答下列问题:
(1)若用系统抽样的方法抽取50个样本,
现将所有学生随机地编号为000,001,002,…,799,试写出第二组第一位学生的编号 ;
(2)填充频率分布表的空格1 2 3 4 并作出频率分布直方图;
(3)若成绩在85.5~95.5分的学生为二等奖,问参赛学生中获得二等奖的学生约有多少人?
一袋中有同样大小的球10个,其中有8个标有1元钱,2个标有5元钱,交5元钱,可以参加一次摸奖,摸奖者只能从中任取2个球,他所得奖励是所抽2球的钱数之和,求抽奖人获利的数学期望.
某气象站天气预报的准确率为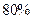 ,计算(结果保留到小数点后面第2位)
,计算(结果保留到小数点后面第2位)
(1)5次预报中恰有2次准确的概率;
(2)5次预报中至少有2次准确的概率;
(3)5次预报中恰有2次准确,且其中第 次预报准确的概率
次预报准确的概率
一名学生每天骑自行车上学,从家到学校的途中有5个交通岗,假设他在各交通岗遇到红灯的事件是相互独立的,并且概率都是 .
.
(1)求这名学生在途中遇到红灯的次数ξ的分布列;
(2)求这名学生在首次遇到红灯或到达目的地停车前经过的路口数η的分布列;
(3)这名学生在途中至少遇到一次红灯的概率.
1
甲、乙、丙三台机床各自独立地加工同一种零件,已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率为 ,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为
,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为 ,甲、丙两台机床加工的零件都是一等品的概率为
,甲、丙两台机床加工的零件都是一等品的概率为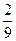
(1)分别求甲、乙、丙三台机床各自加工零件是一等品的概率;
(2)从甲、乙、丙加工的零件中各取一个检验,求至少有一个一等品的概率.
一份航空意外伤害保险保险费为20元,保险金额为45万元.如果某城市的一家保险公司一年能销售这种保单10万份,所需成本为5万元,而需要赔付的概率为 .那么请问1年内赔付人数为多少时,这家保险公司会亏本?
.那么请问1年内赔付人数为多少时,这家保险公司会亏本?