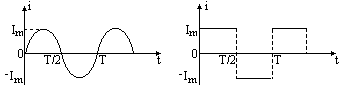
在两个阻值相同的电阻上分别通以如图所示的正弦交变电流和方形波电流,它们的峰值和周期都相同,求两电阻在相同时间内产生的热量之比
如图所示为两组平行板金属板,一组竖直放置,一组水平放置,今有一质量为m、电量为q的电子静止在竖直放置的平行金属板的A点,经电压U0加速后通过B点进入两板间距为d、电压为U的水平放置的平行金属板间,若电子从两块水平平行板的正中间射入,且最后电子刚好能从右侧的两块平行金属板穿出,A、B分别为两块竖直板的中点,求: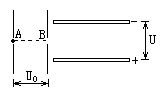
(1)电子通过B点时的速度大小;
(2)右侧平行金属板的长度;
(3)电子穿出右侧平行金属板时的动能。
两个正点电荷Q1=Q和Q2=4Q分别置于固定在光滑绝缘水平面上的A、B两点,A、B两点相距L,且A、B两点正好位于水平放置的光滑绝缘半圆细管两个端点的出口处,如图所示。
现将另一正点电荷置于A、B连线上靠近A处静止释放,求它在AB连线上运动过程中达到最大速度时的位置离A点的距离。
若把该点电荷放于绝缘管内靠近A点处由静止释放,已知它在管内运动过程中速度为最大时的位置在P处。试求出图中PA和AB连线的夹角θ。
.绝缘细绳的一端固定在天花板上,另一端连接着一个带负电的电量为q、质量为m的小球,当空间中有水平方向的匀强电场后,长为L的绳稳定在与竖直方向成θ=300角的A位置,如图所示。求:
匀强电场的场强E;
将小球从O点由静止释放,则到A处时电场力做的功为多少?
小球由静止从O点运动到A点过程中,电势能减少了多少?
如图所示,质量M = 1kg的木板静止在粗糙的水平地面上,木板与地面间的动摩擦因数μ1=0.1,在木板的左端放置一个质量m=1kg、大小可以忽略的铁块,铁块与木板间的动摩擦因数μ2=0.4,取g=10m/s2,试求:

(1)若木板长L=1m,在铁块上加一个水平向右的恒力F=8N,经过多长时间铁块运动到木板的右端?
(2)若在木板(足够长)的右端施加一个大小从零开始连续增加的水平向左的力F,请在图中画出铁块受到的摩擦力f随拉力F大小变化的图像.
 |
4×100m接力赛是奥运会上最为激烈的比赛项目,有甲乙两运动员在训练交接棒的过程中发现,甲短距离加速后能保持9m/s的速度跑完全程.为了确定乙起跑的时机,需在接力区前适当的位置设置标记,在某次练习中,甲在接力区前s0 处作了标记,当甲跑到此标记时向乙发出起跑口令,乙在接力区的前端听到口令时立即起跑(忽略声音传播的时间及人的反应时间),已知接力区的长度为L=20m,设乙起跑后的运动是匀加速运动,试求:
(1)若s0 =13.5m,且乙恰好在速度达到与甲相同时被甲追上,完成交接棒,则在完成交接棒时乙离接力区末端的距离为多大?
(2)若s0 =16m,乙的最大速度为8m/s,并能以最大速度跑完全程,要使甲乙能在接力区完成交接棒,则乙在听到口令后加速的加速度最大为多少?