已知数列 的前
的前 项和为
项和为 ,对一切正整数
,对一切正整数 ,点
,点 都在函数
都在函数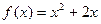 的图象上,且过点
的图象上,且过点 的切线的斜率为
的切线的斜率为 .
.
(1)求数列 的通项公式;(2)若
的通项公式;(2)若 ,求数列
,求数列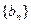 的前
的前 项和
项和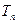 ;
;
(3)设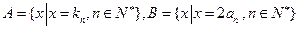 ,等差数列
,等差数列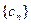 的任一项
的任一项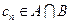 ,其中
,其中 是
是 中的最小数,
中的最小数,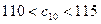 ,求
,求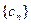 的通项公式.
的通项公式.
设有两个命题.命题p:不等式x2-(a+1)x+1≤0的解集是∅;命题q:函数f(x)=(a+1)x在定义域内是增函数.如果p∧q为假命题,p∨q为真命题,求a的取值范围.
已知p:方程x2+mx+1=0有两个不等的负根;q:方程4x2+4(m-2)x+1=0无实根,若p或q为真,p且q为假,求m的取值范围.
写出由下列各组命题构成的“p或q”、“p且q”、“ p”形式的复合命题,并判断真假.
p”形式的复合命题,并判断真假.
(1)p:1是质数;q:1是方程x2+2x-3=0的根;
(2)p:平行四边形的对角线相等;q:平行四边形的对角线互相垂直;
(3)p:0∈∅;q:{x|x2-3x-5<0}⊆R;
(4)p:5≤5;q:27不是质数.
已知数列{an}的前n项和为Sn=(n+1)2+c,探究{an}是等差数列的充要条件.
已知P={x|a-4<x<a+4},Q={x|x2-4x+3<0},若x∈P是x∈Q的必要条件,求实数a的取值范围.