写出由下列各组命题构成的“p或q”、“p且q”、“
p”形式的复合命题，并判断真假．
(1)p：1是质数；q：1是方程x2＋2x－3＝0的根；
(2)p：平行四边形的对角线相等；q：平行四边形的对角线互相垂直；
(3)p：0∈∅；q：{x|x2－3x－5<0}⊆R；
(4)p：5≤5；q：27不是质数．
已知数列
是等差数列，其前n项和为
（I）求数列的通项公式；
（II）设p、q是正整数，且p≠q．证明：
．
（本小题满分15分）
已知函数
的图象在
上连续不断，定义：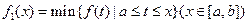 
，
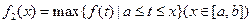
其中，
表示函数在
上的最小值，
表示函数在上的最大值．若存在最小正整数
，使得
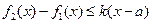对任意的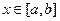
成立，则称函数为上的“阶收缩函数”．
（1）若
，
，试写出
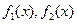的表达式；
（2）已知函数
，
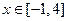，试判断是否为
上的“阶收缩函数”，如果是，求出对应的；如果不是，请说明理由；
（3）已知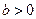
，函数
是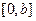
上的2阶收缩函数，求
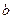的取值范围.
（本小题满分15分）已知椭圆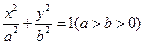
的离心率为
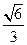，过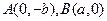
的直线与原点的距离为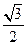
（1）求椭圆的方程；
（2）已知定点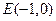
，直线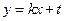
与椭圆交于不同两点C，D，试问：对任意的
，是否都存在实数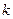
，使得以线段CD为直径的圆过点E？证明你的结论
(本小题满分14分)
等差数列
的前
项和为
，且
（1）求的通项公式
；
（2）若数列满足
且
求
的前项和
本小题满分14分)
经市场调查，某旅游城市在过去的一个月内（以30天计），日旅游人数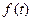
（万人）与时间
（天）的函数关系近似满足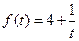
，日人均消费
（元）与时间（天）的函数关系近似满足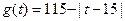
（1）求该城市的旅游日收益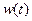
（万元）与时间
的函数关系式；
（2）求该城市旅游日收益的最小值（万元）