如图所示,在光滑水平面上有两辆车处于静止状态,其上分别站有甲、乙两个小孩,每辆车和小孩的总质量均为M,甲车上的小孩拿着一质量为m的球。现小孩甲将球抛给乙,乙接住后又抛回给甲,如此重复多次,最后球又回到了甲的手中,求甲、乙两车最后的速率之比。
利用如图7所示的装置测量滑块和滑板间的动摩擦因数。将质量为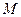 的滑块
的滑块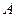 放在倾斜滑板
放在倾斜滑板 上,
上,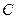 为位移传感器,它能将滑块
为位移传感器,它能将滑块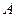 到传感器
到传感器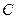 的距离数据实时传送到计算机上,经计算机处理后在屏幕上显示出滑块
的距离数据实时传送到计算机上,经计算机处理后在屏幕上显示出滑块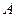 的速度——时间(
的速度——时间(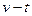 )图像。先给滑块
)图像。先给滑块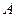 一个沿滑板
一个沿滑板 向上的初速度,得到的
向上的初速度,得到的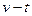 如图8所示,求:
如图8所示,求:
(1)滑块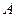 上滑时加速度的大小;
上滑时加速度的大小;
(2)滑块与滑板之间的动摩擦因数(取重力加速度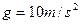 )。
)。
)如图11所示,倾角30°的光滑斜面上,并排放着质量分别是mA=10kg和mB=2kg的A、B两物块,一个劲度系数k=400N/m的轻弹簧一端与物块B相连,另一端与固定挡板相连,整个系统处于静止状态,现对A施加一沿斜面向上的力F,使物块A沿斜面向上作匀加速运动,已知力F在前0.2s内为变力,0.2s后为恒力,g取10m/s2,求F的最大值和最小值。
如图10所示,利用皮带运输机将物体由地面运送到高出水平地面的C平台上,C平台离地面的竖直高度为5m,已知皮带和物体问的动摩擦因数为0.75,运输机的皮带以2m/s的速度匀速顺时针运动且皮带和轮子之间不打滑(g=l0m/s2,sin37°=0.6)。
(1)假设皮带在运送物体的过程中始终是张紧的。为了将地面上的物体能够运送到平台上,皮带的倾角θ最大不能超过多少?
(2)皮带运输机架设好之后,皮带与水平面的夹角为θ=30°,现将质量为l kg的小物体轻轻地放在皮带的A处,运送到C处.试求所需要的时间是多少?
供电局某工程队在冬天架设电线,如图9所示,设两电线杆间距离为L,铜导线总质量为M,电线架好后,在两杆正中部位电线下坠的距离为h,电线在杆上固定磁瓶处的切线方向与竖直方向的夹角为θ,求:
(1)两电线杆处的电线所受弹力多大?
(2)电线最低点A处的张力多大?
(3)当到夏天时,两电线杆处的电线弹力与冬天相比是变大了,还是变小了?为什么?
 一小球作平抛运动,在下落过程中刚好能通过宽为L,高为H的长方形窗户ABCD的对角A和C,所用时间为T,重力加速度为g。求①小球从抛出到经过窗户的上边缘所用的时间。②小球通过C点的速度大小。
一小球作平抛运动,在下落过程中刚好能通过宽为L,高为H的长方形窗户ABCD的对角A和C,所用时间为T,重力加速度为g。求①小球从抛出到经过窗户的上边缘所用的时间。②小球通过C点的速度大小。