双曲线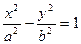 (a>1,b>0)的焦距为2c,直线l过点(a,0)和(0,b),且点(1,0)到直线l的距离与点(-1,0)到直线l的距离之和s≥
(a>1,b>0)的焦距为2c,直线l过点(a,0)和(0,b),且点(1,0)到直线l的距离与点(-1,0)到直线l的距离之和s≥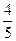 c.求双曲线的离心率e的取值范围.
c.求双曲线的离心率e的取值范围.
已知向量
 .
.
(1)当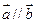 时,求
时,求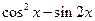 的值;
的值;
(2)设函数 ,已知在△ABC中,内角A、B、C的对边分别为
,已知在△ABC中,内角A、B、C的对边分别为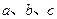 ,若
,若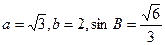 ,求
,求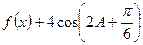 (
( )的取值范围.
)的取值范围.
已知直线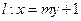 过椭圆
过椭圆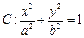 的右焦点F,抛物线:
的右焦点F,抛物线: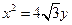 的焦点为椭圆
的焦点为椭圆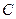 的上顶点,且直线
的上顶点,且直线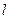 交椭圆
交椭圆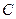 于
于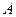 、
、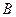 两点,点
两点,点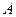 、F、
、F、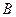 在直线
在直线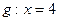 上的射影依次为点
上的射影依次为点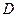 、
、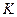 、
、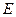 .
.
(1)求椭圆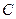 的方程;
的方程;
(2)若直线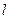 交y轴于点
交y轴于点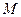 ,且
,且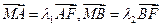 ,当
,当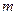 变化时,探求
变化时,探求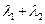
的值是否为定值?若是,求出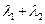 的值,否则,说明理由;
的值,否则,说明理由;
(3)连接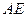 、
、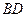 ,试探索当
,试探索当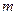 变化时,直线
变化时,直线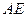 与
与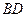 是否相交于定点?
是否相交于定点?
已知函数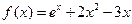 .
.
(1)求证函数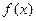 在区间
在区间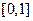 上存在唯一的极值点,并用二分法求函数取得极值时相应
上存在唯一的极值点,并用二分法求函数取得极值时相应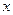 的近似值(误差不超过
的近似值(误差不超过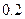 );(参考数据
);(参考数据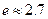 ,
,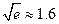 ,
,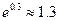 )
)
(2)当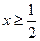 时,若关于
时,若关于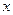 的不等式
的不等式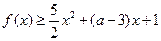 恒成立,试求实数
恒成立,试求实数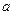 的取值范围.
的取值范围.
已知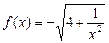 ,数列
,数列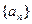 的前n项和为
的前n项和为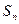 ,点
,点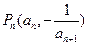
 在曲线
在曲线 上
上 ,且
,且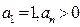 。
。
(1)求数列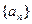 的通项公式;
的通项公式;
(2)数列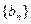 的前n项和为
的前n项和为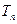 ,且满足
,且满足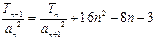 ,
,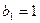 ,
,
求证:数列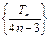 是等差数列,并求数列
是等差数列,并求数列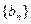 的通项公式;
的通项公式;
如图,三棱锥P-ABC中,PA⊥底面ABC,AB⊥BC,DE垂直平分线段PC,且分别交AC、PC于D、E两点,又PB =BC,PA=AB。
=BC,PA=AB。
(1)求证:PC⊥平面BDE;
(2)若点Q是线段PA上任一点,判断BD、DQ的位置关系,并证明你的结论;
(3)若AB=2,求三棱锥B-CED的体积