某服装加工厂对外批发某种服装,生产成本为每件40元,对外批发价定为每件60元.该加工厂为了鼓励零售商大批量购买,推出优惠政策:一次购买不超过50件时,只享受批发价;一次购买超过50件时,每多购买1件,购买者所购买的所有服装可在享受批发价的基础上,每件再降低0.2元,但每件最低价不低于50元.
(1)试写出该种服装实际售价 与销售数量
与销售数量 的函数关系式;
的函数关系式;
(2)在每件实际售价高于50元时,购买者一次购买多少件,加工厂获得的利润最大?
(利润=销售总额-成本)
自点A(-3,3)发出的光线L射到x轴上,被x轴反射,其反射光线所在直线与圆x2+y2-4x-4y+7=0相切,求光线L所在直线的方程。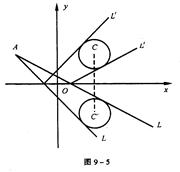
已知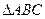 的顶点
的顶点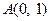 ,
,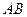 边上的中线
边上的中线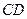 所在的直线方程为
所在的直线方程为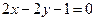 ,
,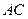 边上的高
边上的高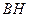 所在直线的方程为
所在直线的方程为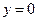 .
.
(1)求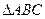 的顶点
的顶点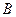 、
、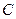 的坐标;
的坐标;
(2)若圆 经过不同的三点
经过不同的三点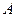 、
、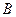 、
、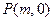 ,且斜率为
,且斜率为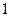 的直线与圆
的直线与圆 相切于点
相切于点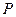 ,求圆
,求圆 的方程.
的方程.
设椭圆的中心在原点,焦点在x轴上,离心率e=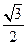 .已知点P
.已知点P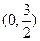 到这个椭圆上的点的最远距离为
到这个椭圆上的点的最远距离为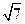 ,求这个椭圆的方程.
,求这个椭圆的方程.
已知圆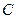 和
和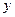 轴相切,圆心在直线
轴相切,圆心在直线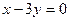 上,且被直线
上,且被直线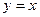 截得的弦长为
截得的弦长为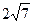
 ,求圆
,求圆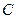 的方程。
的方程。
已知椭圆C的中心在坐标原点,焦点在x轴上,离心率为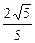 ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线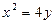 的焦点。
的焦点。
(1)求椭圆C的标准方程;
(2)过椭圆C的右焦点作直线l交椭圆C于A、B两点,交y轴于M点,若 的值。
的值。