已知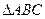 的顶点
的顶点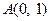 ,
,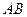 边上的中线
边上的中线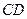 所在的直线方程为
所在的直线方程为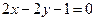 ,
,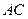 边上的高
边上的高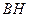 所在直线的方程为
所在直线的方程为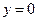 .
.
(1)求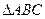 的顶点
的顶点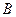 、
、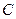 的坐标;
的坐标;
(2)若圆 经过不同的三点
经过不同的三点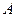 、
、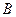 、
、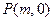 ,且斜率为
,且斜率为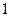 的直线与圆
的直线与圆 相切于点
相切于点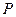 ,求圆
,求圆 的方程.
的方程.
为适应新课改,切实减轻学生负担,提高学生综合素质,某市某学校高三年级文科生300人在数学选修4-4、4-5、4-7选课方面进行改革,由学生自由选择2门(不可多选或少选),选课情况如下表:
| 4-4 |
4-5 |
4-7 |
|
| 男生 |
130 |
 |
80 |
| 女生 |
 |
100 |
60 |
(1)为了解学生情况,现采用分层抽样方法抽取了三科作业共50本,统计发现4-5有18本,试根据这一数据求出 ,
, 的值.
的值.
(2)为方便开课,学校要求 ≥110,
≥110, >110,计算
>110,计算 >
> 的概率.
的概率.
设函数 ,且以
,且以 为最小正周期.
为最小正周期.
(1)求 的值;
的值;
(2)已知 ,求
,求 的值.
的值.
已知 都是正数,且
都是正数,且 成等比数列,求证:
成等比数列,求证:
已知曲线C1的极坐标方程为 ,曲线C2的极坐标方程为
,曲线C2的极坐标方程为 ,曲线C1,C2相交于A,B两点
,曲线C1,C2相交于A,B两点
(I)把曲线C1,C2的极坐标方程转化为直角坐标方程;
(II)求弦AB的长度.
圆O是 的外接圆,过点C的圆的切线与AB的延长线交于点D,
的外接圆,过点C的圆的切线与AB的延长线交于点D, ,
,
AB=BC=3,求BD以及AC的长.