为适应新课改,切实减轻学生负担,提高学生综合素质,某市某学校高三年级文科生300人在数学选修4-4、4-5、4-7选课方面进行改革,由学生自由选择2门(不可多选或少选),选课情况如下表:
| |
4-4 |
4-5 |
4-7 |
| 男生 |
130 |
 |
80 |
| 女生 |
 |
100 |
60 |
(1)为了解学生情况,现采用分层抽样方法抽取了三科作业共50本,统计发现4-5有18本,试根据这一数据求出 ,
, 的值.
的值.
(2)为方便开课,学校要求 ≥110,
≥110, >110,计算
>110,计算 >
> 的概率.
的概率.
【改编】(本小题满分12分)贵广高速铁路自贵阳北站起,经黔南州、黔东南、广西桂林、贺州、广东肇庆、佛山终至广州南站.其中广东省内有怀集站、广宁站、肇庆东站、三水南站、佛山西站、广州南站共6个站.记者对广东省内的6个车站随机抽取3个进行车站服务满意度调查.
(1)求抽取的车站中不含佛山市内车站(包括三水南站和佛山西站)的概率;
(2)设抽取的车站中含有肇庆市内车站(包括怀集站、广宁站、肇庆东站)个数为X,求X的分布列及其均值(即数学期望).
对于函数 ,若
,若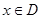 时,恒有
时,恒有 成立,则称函数
成立,则称函数 是
是 上 的“
上 的“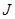 函数”.
函数”.
(Ⅰ)当函数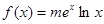 是定义域上的“
是定义域上的“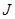 函数”时,求实数
函数”时,求实数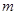 的取值范围;
的取值范围;
(Ⅱ)若函数 为
为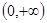 上的“
上的“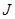 函数”.
函数”.
(ⅰ)试比较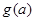 与
与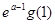 的大小(其中
的大小(其中 );
);
(ⅱ)求证:对于任意大于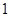 的实数
的实数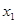 ,
, ,
,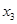 ,,
,,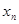 均有
均有 .
.
(本小题满分13分)已知椭圆 的离心率为
的离心率为 ,且过点
,且过点 .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)四边形ABCD的顶点在椭圆上,且对角线AC,BD过原点O,设 ,满足
,满足 .
.
(ⅰ)试证 的值为定值,并求出此定值;
的值为定值,并求出此定值;
(ⅱ)试求四边形ABCD面积的最大值.
(本小题满分12分)如图, 垂直于梯形
垂直于梯形 所在的平面,
所在的平面, .
. 为
为 中点,
中点, ,
, 四边形
四边形 为矩形,线段
为矩形,线段 交
交 于点N .
于点N .
(1)求证: // 平面
// 平面 ;
;
(2)求二面角 的大小;
的大小;
(3)在线段 上是否存在一点
上是否存在一点 ,使得
,使得 与平面
与平面 所成角的大小为
所成角的大小为 ? 若存在,请求出
? 若存在,请求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
(本小题满分12分)已知在数列 中,
中, ,
, ,
, .
.
(1)证明数列 是等差数列,并求
是等差数列,并求 的通项公式;
的通项公式;
(2)设数列 的前
的前 项和为
项和为 ,证明:
,证明: .
.