抽取某种型号的车床生产的10个零件，编号为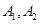
，…，
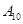，测量其直径（单位：cm），得到下面数据：
| 编号 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
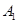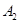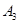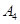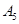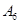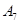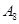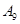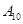| 直径 |
1．51 |
1．49 |
1．49 |
1．51 |
1．49 |
1．48 |
1．47 |
1．53 |
1．52 |
1．47 |
其中直径在区间［1．49，1．51］内的零件为一等品．
（1）从上述10个零件中，随机抽取一个，求这个零件为一等品的概率；
（2）从一等品零件中，随机抽取2个．
①用零件的编号列出所有可能的抽取结果；
②求这2个零件直径相等的概率；
（3）若甲、乙分别从一等品中各取一个，求甲取到零件的直径大于乙取到零件的直径的概率．
（本小题满分12分）
已知数列
是等比数列，
，且
是
的等差中项.
(Ⅰ) 求数列的通项公式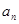
；
（Ⅱ）若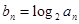
，求数列
的前n项和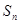
.
（本小题满分10分）
在
中，
(Ⅰ)求
的值 ；（Ⅱ）求
的值。
已知函数
.
(Ⅰ)若曲线
在
和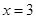
处的切线互相平行，求
的值；
(Ⅱ)求
的单调区间；
(Ⅲ)设
，若对任意
，均存在
，使得
，求的取值范围.
在平面直角坐标系
中，点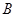
与点A（-1,1）关于原点O对称，P是动点，且直线AP与BP的斜率之积等于
.
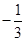(Ⅰ)求动点P的轨迹方程；
(Ⅱ)设直线AP和BP分别与直线
交于点M,N，问：是否存在点P使得△PAB与△PMN的面积相等？若存在，求出点P的坐标；若不存在，说明理由。
已知抛物线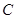
:
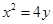的焦点为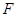
,
、
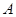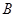是抛物线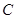上异于坐标原点
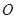的不同两点，抛物线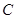在点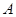、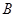处的切线分别为
、
，且
，与相交于点
. 
(1) 求点的纵坐标；
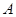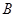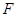(2) 证明：、、三点共线；