(本小题满分12分)
设函数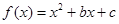 ,其中
,其中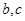 是某范围内的随机数,分别在下列条件下,求事件A “
是某范围内的随机数,分别在下列条件下,求事件A “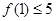 且
且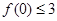 ”发生的概率.
”发生的概率.
(Ⅰ)若随机数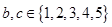 ;
;
(Ⅱ)已知随机函数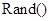 产生的随机数的范围为
产生的随机数的范围为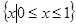 ,
,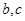 是算法语句
是算法语句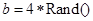 和
和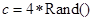 的执行结果.(注: 符号“
的执行结果.(注: 符号“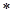 ”表示“乘号”)
”表示“乘号”)
某高校在2012年自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示.
(1)分别求第3,4,5组的频率;
(2) 若该校决定在笔试成绩较高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试。
(ⅰ) 已知学生甲和学生乙的成绩均在第三组,求学生甲和学生乙恰有一人进入第二轮面试的概率;
(ⅱ) 学校决定在这已抽取到的6名学生中随机抽取2名学生接受考官L的面试,设第4组中有 名学生被考官L面试,求
名学生被考官L面试,求 的分布列和数学期望.
的分布列和数学期望.
若 的图像与直线
的图像与直线 相切,并且切点横坐标依次成公差为
相切,并且切点横坐标依次成公差为 的等差数列.
的等差数列.
(1)求 和
和 的值;
的值;
(2) ⊿ABC中,a、b、c分别是∠A、∠B、∠C的对边。若 是函数
是函数 图象的一个对称中心,且a=4,求⊿ABC外接圆的面积。
图象的一个对称中心,且a=4,求⊿ABC外接圆的面积。
选修4-5:不等式选讲
已知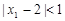 ,
,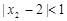 .
.
(I)求证: ,
,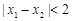 ;
;
(II)若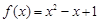 ,求证:
,求证: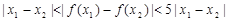
选修4-4:坐标系与参数方程
在极坐标系中, O为极点, 半径为2的圆C的圆心的极坐标为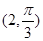 .
.
⑴求圆C的极坐标方程;
⑵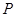 是圆
是圆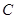 上一动点,点
上一动点,点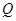 满足
满足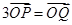 ,以极点O为原点,以极轴为x轴正半轴建立直角坐标系,求点Q的轨迹的直角坐标方程.
,以极点O为原点,以极轴为x轴正半轴建立直角坐标系,求点Q的轨迹的直角坐标方程.
选修4-1:几何证明选讲
如图,AB、CD是圆的两条平行弦,BE//AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.
(I)求AC的长;
(II)求证:BE=EF.