(本小题满分10分)选修4—5:不等式选讲
已知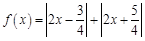 .
.
(1)关于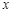 的不等式
的不等式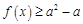 恒成立,求实数
恒成立,求实数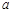 的取值范围;
的取值范围;
(2)设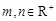 ,且
,且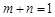 ,求证:
,求证: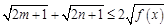 .
.
(本小题满分10分)选修4—4:极坐标与参数方程
在直角坐标系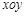 中,直线
中,直线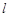 的参数方程为
的参数方程为 (
( 为参数).再以原点为极点,以
为参数).再以原点为极点,以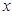 正半轴为极轴建立极坐标系,并使得它与直角坐标系
正半轴为极轴建立极坐标系,并使得它与直角坐标系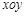 有相同的长度单位.在该极坐标系中圆
有相同的长度单位.在该极坐标系中圆 的方程为
的方程为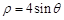 .
.
(1)求圆 的直角坐标方程;
的直角坐标方程;
(2)设圆 与直线
与直线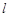 交于点
交于点 、
、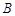 ,若点
,若点 的坐标为
的坐标为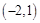 ,求
,求 的值.
的值.
(本小题满分10分)选修4—1:几何证明选讲
如图,正方形 边长为2,以
边长为2,以 为圆心、
为圆心、 为半径的圆弧与以
为半径的圆弧与以 为直径的半圆
为直径的半圆 交于点
交于点 ,连结
,连结 并延长交
并延长交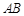 于点
于点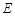 .
.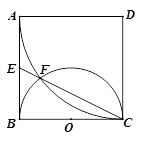
(1)求证: ;
;
(2)求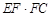 的值.
的值.
(本小题满分12分)已知函数 .
.
(Ⅰ)设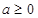 ,求
,求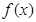 的单调区间;
的单调区间;
(Ⅱ) 设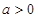 ,且对于任意
,且对于任意 ,
, .试比较
.试比较 与
与 的大小.
的大小.
(本小题满分12分)已知圆C过点P(1,1),且与圆M: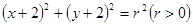 关于直线
关于直线 对称.
对称.
(1)求圆C的方程:
(2)设Q为圆C上的一个动点,求 最小值;
最小值;
(3)过点P作两条相异直线分别与圆C交与A,B,且直线PA和直线PB的倾斜角互补,O为坐标原点,试判断直线OP与直线AB是否平行?请说明理由.