已知函数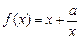 的定义域为
的定义域为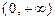 ,且
,且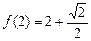 . 设点
. 设点 是函数图象上的任意一点,过点
是函数图象上的任意一点,过点 分别作直线
分别作直线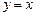 和
和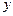 轴的垂线,垂足分别为
轴的垂线,垂足分别为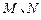 .
.
(1)求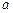 的值;
的值;
(2)问: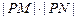 是否为定值?若是,则求出该定值,若不是,则说明理由;
是否为定值?若是,则求出该定值,若不是,则说明理由;
(3)设 为坐标原点,求四边形
为坐标原点,求四边形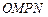 面积的最小值.
面积的最小值.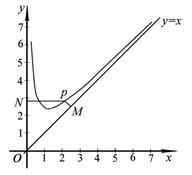
设函数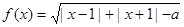
(Ⅰ)当 时,求函数
时,求函数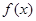 的定义域;
的定义域;
(Ⅱ)若函数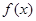 的定义域为
的定义域为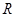 ,求实数
,求实数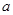 的取值范围.
的取值范围.
已知直线: (为参数);椭圆
(为参数);椭圆 :
: (
( 为参数)
为参数)
(Ⅰ)求直线倾斜角的余弦值;
(Ⅱ)试判断直线与椭圆 的交点个数.
的交点个数.
已知矩阵 有特征值
有特征值 及对应特征向量
及对应特征向量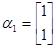 ,且矩阵
,且矩阵 对应的变换将点
对应的变换将点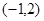 变换成
变换成
(Ⅰ)求矩阵 ;
;
(Ⅱ)若直线在矩阵 所对应的线性变换作用下得到直线
所对应的线性变换作用下得到直线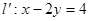 ,求直线方程.
,求直线方程.
持续性的雾霾天气严重威胁着人们的身体健康,汽车的尾气排放是造成雾霾天气的重要因素之一.为此,某城市实施了机动车尾号限行,该市报社调查组为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
| 年龄(岁) |
[15,25) |
[25,35) |
[35,45) |
[45,55) |
[55,65) |
[65,75] |
| 频数 |
5 |
10 |
15 |
10 |
5 |
5 |
| 支持的人数 |
4 |
6 |
9 |
6 |
3 |
4 |
(Ⅰ)请估计该市公众对“车辆限行”的支持率和被调查者的年龄平均值;
(Ⅱ)若从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行追踪调查,记被选4人中不支持“车辆限行”的人数为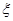 ,求随机变量
,求随机变量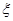 的分布列;
的分布列;
(Ⅲ)若在这50名被调查者中随机发出20份的调查问卷,记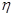 为所发到的20人中赞成“车辆限行”的人数,求使概率
为所发到的20人中赞成“车辆限行”的人数,求使概率 取得最大值的整数
取得最大值的整数 .
.
一个盒子中装有5张卡片,每张卡片上写有一个数字,数字分别是1、2、3、4、5,现从盒子中随机抽取卡片.
(1)从盒中依次抽取两次卡片,每次抽取一张,取出的卡片不放回,求两次取到的卡片的数字既不全是奇数,也不全是偶数的概率;
(2)若从盒子中有放回的抽取3次卡片,每次抽取一张,求恰有两次取到卡片的数字为偶数的概率;
(3)从盒子中依次抽取卡片,每次抽取一张,取出的卡片不放回,当抽到记有奇数的卡片即停止抽取,否则继续抽取卡片,求抽取次数X的分布列和期望.