一个盒子中装有5张卡片,每张卡片上写有一个数字,数字分别是1、2、3、4、5,现从盒子中随机抽取卡片.
(1)从盒中依次抽取两次卡片,每次抽取一张,取出的卡片不放回,求两次取到的卡片的数字既不全是奇数,也不全是偶数的概率;
(2)若从盒子中有放回的抽取3次卡片,每次抽取一张,求恰有两次取到卡片的数字为偶数的概率;
(3)从盒子中依次抽取卡片,每次抽取一张,取出的卡片不放回,当抽到记有奇数的卡片即停止抽取,否则继续抽取卡片,求抽取次数X的分布列和期望.
出租车司机从饭店到火车站途中有六个交通岗,假设他在各交通岗到红灯这一事件是相互独立的,并且概率都是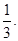
(1)求这位司机遇到红灯前,已经通过了两个交通岗的概率;
(2)求这位司机在途中遇到红灯数ξ的期望和方差。
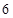 个人坐在一排
个人坐在一排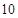 个座位上,问(1)空位不相邻的坐法有多少种?
个座位上,问(1)空位不相邻的坐法有多少种?
(2) 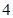 个空位只有
个空位只有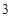 个相邻的坐法有多少种?
个相邻的坐法有多少种?
(3) 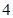 个空位至多有
个空位至多有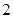 个相邻的坐法有多少种?
个相邻的坐法有多少种?
甲乙两人独立解某一道数学题,已知该题被甲独立解出的概率为 ,被甲或乙解出的概率为
,被甲或乙解出的概率为 ,(1)求该题被乙独立解出的概率;
,(1)求该题被乙独立解出的概率;
(2)求解出该题的人数 的数学期望和方差
的数学期望和方差
如图,在直三棱柱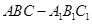 中,
中,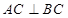 ,点
,点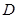 是
是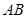 的中点.
的中点.
求证:(1)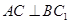 ;(2)
;(2)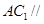 平面
平面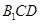 .
.
设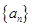 是公差为正数的等差数列,若
是公差为正数的等差数列,若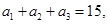
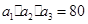 ,
,
求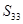 。
。