甲、乙两人进行某项对抗性游戏,采用“七局四胜”制,即先赢四局者为胜,若甲、乙两人水平相当,且已知甲先赢了前两局,求:
(1)乙取胜的概率;
(2)比赛进行完七局的概率。
(3)记比赛局数为 ,求
,求 的分布列为数学期望
的分布列为数学期望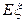 .
.
已知函数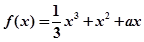 .
.
(1)若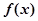 在区间
在区间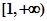 单调递增,求
单调递增,求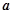 的最小值;
的最小值;
(2)若 ,对
,对 ,使
,使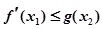 成立,求
成立,求 的范围.
的范围.
如图四棱锥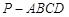 中,底面
中,底面 是平行四边形,
是平行四边形,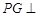 平面
平面 ,垂足为
,垂足为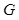 ,
, 在
在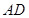 上且
上且 ,
, ,
, ,
, 是
是 的中点,四面体
的中点,四面体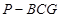 的体积为
的体积为 .
.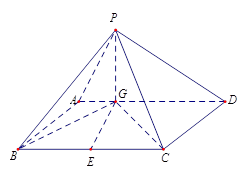
(1)求过点P,C,B,G四点的球的表面积;
(2)求直线 到平面
到平面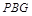 所成角的正弦值;
所成角的正弦值;
(3)在棱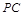 上是否存在一点
上是否存在一点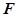 ,使
,使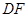

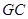 ,若存在,确定点
,若存在,确定点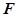 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.
甲乙两人拿两颗骰子做投掷游戏,规则如下:若掷出的点数之和为3的倍数,原掷骰子的人再继续掷,否则,由对方接着掷。第一次由甲开始掷。
(1)分别求第二次、第三次由甲掷的概率;
(2)求前4次抛掷中甲恰好掷两次的概率.
已知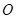 为坐标原点,
为坐标原点, ,
, .
.
(Ⅰ)若 的定义域为
的定义域为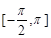 ,求
,求 的单调递增区间;
的单调递增区间;
(Ⅱ)若 的定义域为
的定义域为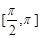 ,值域为
,值域为 ,求
,求 的值.
的值.
定义函数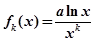 为
为 的
的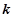 阶函数.
阶函数.
(1)求一阶函数 的单调区间;
的单调区间;
(2)讨论方程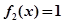 的解的个数;
的解的个数;
(3)求证: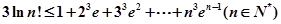 .
.