某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响. 已知某学生只选修甲的概率为 ,只选修甲和乙的概率是
,只选修甲和乙的概率是 ,至少选修一门的概率是
,至少选修一门的概率是 ,用
,用 表示该学生选修的课程门数和没有选修的课程门数的乘积.
表示该学生选修的课程门数和没有选修的课程门数的乘积.
(1)记“函数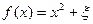
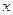 为
为 上的偶函数”为事件
上的偶函数”为事件 ,求事件
,求事件 的概率;
的概率;
(2)求 的分布列和数学期望.
的分布列和数学期望.
(本题10分)在等比数列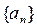 中,
中,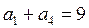 ,
,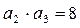 ,
,
求数列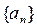 的前6项和
的前6项和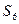 .
.
已知函数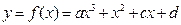 是定义在R上的函数,其图象与x轴的一个交点
是定义在R上的函数,其图象与x轴的一个交点
为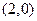 ,若函数
,若函数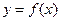 的图象在
的图象在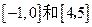 上是减函数,在
上是减函数,在 上是增函数。
上是增函数。
(1)求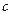 的值;
的值;
(2)求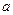 的取值范围;
的取值范围;
(3)在函数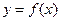 的图象上是否存在一点
的图象上是否存在一点 ,使得曲线
,使得曲线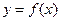 在点
在点 处的切线
处的切线
的斜率为3?若存在,求出点 的坐标;若不存在,说明理由。
的坐标;若不存在,说明理由。
设奇函数 的图像在点
的图像在点 处切线的斜率等于
处切线的斜率等于 ,又
,又 .
.
(1)求函数 的解析式;
的解析式;
(2)设函数 的导函数
的导函数 ,
,
求函数 的单调区间.
的单调区间.
在中央电视台所举办的北京2008年奥运火炬手的一期选拔节目中,假定每个选手需要进行四轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考核,否则即被淘汰。若某选手能正确回答第一、二、三、四轮问题的概率分别是 ,且各轮问题能否正确回答互不影响。
,且各轮问题能否正确回答互不影响。
(1)求该选手进入第四轮才被淘汰的概率;
(2)该选手在选拔过程中,他回答过的问题的总个数记为 ,求随机变量
,求随机变量 的分布列和数学期望.
的分布列和数学期望.
已知数列 的通项公式
的通项公式 ,
,  ,
,
试求 的值,由此推测
的值,由此推测 的计算公式,并用数学归纳法加以证明.
的计算公式,并用数学归纳法加以证明.