已知函数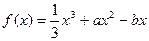 (
(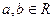 )
)
(1) 若 图象上的点
图象上的点 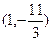 处的切线斜率为
处的切线斜率为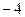 ,求
,求 的极大值;
的极大值;
(2) 若 在区间
在区间 上是单调减函数,求
上是单调减函数,求 的最小值.
的最小值.
如图,在 中,
中, 为
为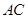 边上的高,
边上的高,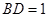 ,
,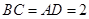 ,沿
,沿 将
将 翻折,使得
翻折,使得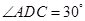 ,得到几何体
,得到几何体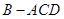 。
。
(1)求证: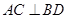 ;
;
(2)求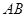 与平面
与平面 所成角的正切值。
所成角的正切值。
如图,直四棱柱ABCD—A1B1C1D1的高为3,底面是边长为4且∠DAB=60°的菱形,AC∩BD=0,A1C1∩B1D1=O1,E是O1A的中点.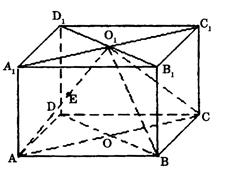
(1)求证:平面O1AC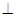 平面O1BD
平面O1BD
(2)求二面角O1-BC-D的大小;
(3)求点E到平面O1BC的距离.
计算并输出1×2×3×4×﹣﹣﹣×n>1000的最小整数n,写出程序框图,并编写程序。
某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是 ,样本数据分组为
,样本数据分组为 ,
,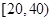 ,
, ,
, ,
, .
.
(Ⅰ)求直方图中 的值;
的值;
(Ⅱ)如果上学所需时间不少于1小时的学生可申请在学校住宿,请估计学校600名新生中有多少名学生可以申请住宿;
已知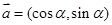 ,
,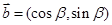 ,其中
,其中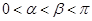
(1)求证: 与
与 互相垂直;
互相垂直;
(2)若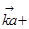
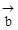 与
与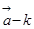
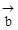 的长度相等,求
的长度相等,求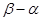 的值(
的值(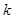 为非零的常数) .
为非零的常数) .