如图,直四棱柱ABCD—A1B1C1D1的高为3,底面是边长为4且∠DAB=60°的菱形,AC∩BD=0,A1C1∩B1D1=O1,E是O1A的中点.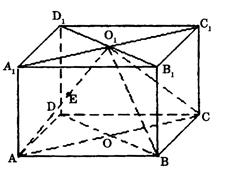
(1)求证:平面O1AC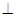 平面O1BD
平面O1BD
(2)求二面角O1-BC-D的大小;
(3)求点E到平面O1BC的距离.
甲、乙两袋中各装有大小相同的小球9个,其中甲袋中红色、黑色、白色小球的个数分别为2、3、4,乙袋中红色、黑色、白色小球的个数均为3,某人用左手从甲袋中取球,用右手从乙袋中取球,
(1)若左右手各取一球,求两只手中所取的球颜色不同的概率;
(2)若一次在同一袋中取出两球,如果两球颜色相同则称这次取球获得成功。某人第一次左手先取两球,第二次右手再取两球,记两次取球的获得成功的次数为随机变量X,求X的分布列和数学期望.
数列 满足:
满足:
(1)记 ,求证:数列
,求证:数列 是等比数列;
是等比数列;
(2)求数列 的通项公式.
的通项公式.
设不等式 的解集为
的解集为 ,
, .
.
(Ⅰ)证明: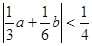 ;
;
(Ⅱ)比较 与
与 的大小,并说明理由.
的大小,并说明理由.
在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系。已知曲线C1的极坐标方程为 ,直线l的极坐标方程为
,直线l的极坐标方程为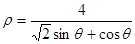 。
。
(Ⅰ)写出曲线C1与直线l的直角坐标方程;
(Ⅱ)设Q为曲线C1上一动点,求Q点到直线l距离的最小值。
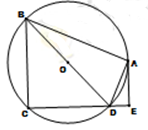
如图,四边形ABCD内接于⊙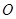 ,
, 是⊙
是⊙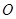 的直径,
的直径, 于点
于点 ,
, 平分
平分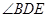 .
.
(Ⅰ)证明: 是⊙
是⊙ 的切线
的切线
(Ⅱ)如果 ,求
,求 .
.